题目内容
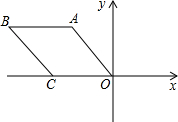 菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=45°,则B点的坐标是
菱形OABC在平面直角坐标系中的位置如图所示,若OA=2,∠AOC=45°,则B点的坐标是(-2-
,
)
| 2 |
| 2 |
(-2-
,
)
.| 2 |
| 2 |
分析:过A作AE⊥CO,根据“OA=2,∠AOC=45°”求出OE、AE的长度,点B的坐标便不难求出.
解答:解:如图,过A作AE⊥CO于E,
∵OA=2,∠AOC=45°,
∴AE=AOsin45°=
,OE=AOcos45°=
,
∴点B的横坐标为-(2+
),纵坐标为
,
∴B点的坐标是(-2-
,
).
故答案为:(-2-
,
).

∵OA=2,∠AOC=45°,
∴AE=AOsin45°=
| 2 |
| 2 |
∴点B的横坐标为-(2+
| 2 |
| 2 |
∴B点的坐标是(-2-
| 2 |
| 2 |
故答案为:(-2-
| 2 |
| 2 |
点评:本题考查了菱形的性质和锐角三角函数,通过作辅助线求出点A到坐标轴的距离是解本题的突破口.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
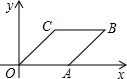 菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC=
菱形OABC在平面直角坐标系中的位置如图所示.∠AOC=45°,OC= (2013•瑶海区一模)每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.
(2013•瑶海区一模)每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示. 秒
秒 如图,菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=
如图,菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,OC=