题目内容
(2011•道外区二模)菱形OABC在平面直角坐标系中的位置如图所示,OA=5,cosB=
,直线AC交y轴于点D,动点P从A出发,以每秒2个单位的速度沿折线A-B-C向终点C匀速运动,同时,动点Q从D点出发,以每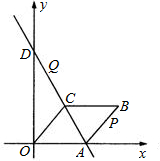 秒
秒
个单位的速度沿DA向终点A匀速运动,设点P、Q运动的时间为t秒.
(1)求点C的坐标;
(2)求△PCQ的面积S(点P在BC上)与运动时间t的函数关系式,并写出自变量的取值范围;
(3)当t=
时,直线PQ交y轴于F点,求
的值.
| 3 |
| 5 |
 秒
秒| 5 |
(1)求点C的坐标;
(2)求△PCQ的面积S(点P在BC上)与运动时间t的函数关系式,并写出自变量的取值范围;
(3)当t=
| 5 |
| 2 |
| FD |
| OD |
分析:(1)由四边形ABCO是菱形我们可以得出角相等和边相等,作CE⊥OA交OA于点E,由cosB=
求出OE的长度,再根据勾股定理就可以求出CE的长度,从而求出C点的坐标.
(2)根据A、C的坐标求出直线AC的解析式,求出AD的长,利用勾股定理求出AC的长,从而求出CD的长度,分为点Q在CD之间和在AC之间时两个不同的解析式.
(3)当t=
时,利用相似可以求出Q、B的坐标,从而可以求出直线PQ的解析式,求出OF的值,从求出其结论.
| 3 |
| 5 |
(2)根据A、C的坐标求出直线AC的解析式,求出AD的长,利用勾股定理求出AC的长,从而求出CD的长度,分为点Q在CD之间和在AC之间时两个不同的解析式.
(3)当t=
| 5 |
| 2 |
解答: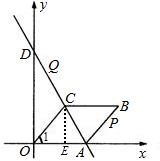 解:(1)作CE⊥OA交OA于点E,
解:(1)作CE⊥OA交OA于点E,
∵四边形ABCO是菱形,
∴OA=AB=BC=CO=5,∠1=∠B,
∵cosB=
,
∴cos∠1=
=
,
∴
=
,
∴OE=3,∴AE=2,
在Rt△OEC和Rt△AEC中,由勾股定理,得
EC=4,CA=2
,
∴C(3,4);
(2)∵OA=5,
∴A(5,0),
设直线AC的解析式为:y=kx+b,由题意,得
,解得
,
∴直线AC的解析式为:y=-2x+10,
当x=0时,y=10,
∴OD=10,在Rt△AOD中由勾股定理,得
AD=5
,
∴CD=3
,
∴当
≤t<3时,
DQ=
t,QA=5
-
t,
∴
=
,
∴
=
,
∴QG=10-2t,
∴S=
,
S=2t2-16t+30,
当3<t<5时,
S=
,
S=-2t2+16t-30;
(3)当t=
时,P(8,4),QG=5,
∴5=-2x+10,
∴x=
,
∴Q(
,5),
设直线PQ的解析式为y=kx+b,由题意,得
,解得
,
∴直线PQ的解析式为y=-
x+
,
当x=0时,y=
,
∴OF=
,
∴FD=
,
∴
=
.
 解:(1)作CE⊥OA交OA于点E,
解:(1)作CE⊥OA交OA于点E,∵四边形ABCO是菱形,
∴OA=AB=BC=CO=5,∠1=∠B,
∵cosB=
| 3 |
| 5 |
∴cos∠1=
| OE |
| OC |
| 3 |
| 5 |
∴
| OE |
| 5 |
| 3 |
| 5 |
∴OE=3,∴AE=2,
在Rt△OEC和Rt△AEC中,由勾股定理,得
EC=4,CA=2
| 5 |
∴C(3,4);
(2)∵OA=5,
∴A(5,0),
设直线AC的解析式为:y=kx+b,由题意,得
|
|
∴直线AC的解析式为:y=-2x+10,
当x=0时,y=10,
∴OD=10,在Rt△AOD中由勾股定理,得
AD=5
| 5 |
∴CD=3
| 5 |
∴当
| 5 |
| 2 |
DQ=
| 5 |
| 5 |
| 5 |
∴
| AQ |
| AD |
| QG |
| OD |
∴
5
| ||||
5
|
| QG |
| 10 |
∴QG=10-2t,
∴S=
| (10-2t)(10-2t-4) |
| 2 |
S=2t2-16t+30,
当3<t<5时,
S=
| (2t-6)(10-2t) |
| 2 |
S=-2t2+16t-30;
(3)当t=
| 5 |
| 2 |
∴5=-2x+10,
∴x=
| 5 |
| 2 |
∴Q(
| 5 |
| 2 |
设直线PQ的解析式为y=kx+b,由题意,得

|
|
∴直线PQ的解析式为y=-
| 2 |
| 11 |
| 60 |
| 11 |
当x=0时,y=
| 60 |
| 11 |
∴OF=
| 60 |
| 11 |
∴FD=
| 50 |
| 11 |
∴
| FD |
| OD |
| 5 |
| 11 |
点评:本题是一道一次函数的综合试题,考查了三角形的面积公式的运用菱形的性质,勾股定理的运用,待定系数法求函数的解析式及解直角三角形的相关知识.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 回答下列问题.
回答下列问题.