题目内容
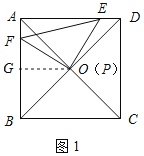
【题目】如图,在正方形ABCD中,对角线AC与BD交于点O,在Rt△PFE中,∠EPF=90°,点E、F分别在边AD、AB上.
(1)如图1,若点P与点O重合:①求证:AF=DE;②若正方形的边长为2![]() ,当∠DOE=15°时,求线段EF的长;
,当∠DOE=15°时,求线段EF的长;
(2)如图2,若Rt△PFE的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,证明:PE=2PF.

【答案】(1)①证明见解析,②![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)①根据正方形的性质和旋转的性质即可证得:△AOF≌△DOE根据全等三角形的性质证明;
②作OG⊥AB于G,根据余弦的概念求出OF的长,根据勾股定理求值即可;
(2)首先过点P作HP⊥BD交AB于点H,根据相似三角形的判定和性质求出PE与PF的数量关系.
(1)①证明:∵四边形ABCD是正方形,
∴OA=OD,∠OAF=∠ODE=45°,∠AOD=90°,
∴∠AOE+∠DOE=90°,
∵∠EPF=90°,
∴∠AOF+∠AOE=90°,
∴∠DOE=∠AOF,
在△AOF和△DOE中,
 ,
,
∴△AOF≌△DOE,
∴AF=DE;
②解:过点O作OG⊥AB于G,
∵正方形的边长为2![]() ,
,
∴OG=![]() BC=
BC=![]() ,
,
∵∠DOE=15°,△AOF≌△DOE,
∴∠AOF=15°,
∴∠FOG=45°-15°=30°,
∴OF=![]() =2,
=2,
∴EF=![]() ;
;
(2)证明:如图2,过点P作HP⊥BD交AB于点H,

则△HPB为等腰直角三角形,∠HPD=90°,
∴HP=BP,
∵BD=3BP,
∴PD=2BP,
∴PD=2HP,
又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°,
∴∠HPF=∠DPE,
又∵∠BHP=∠EDP=45°,
∴△PHF∽△PDE,
∴![]() ,
,
∴PE=2PF.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目