Question

【题目】已知：内接于，，平分.

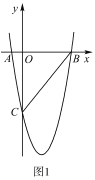
(1)如图，求证：为等边三角形.

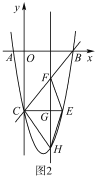
(2)如图，为直径，点在上，于点，交于点，连接，将绕点逆时针旋转使点落在上的点处，求证：；

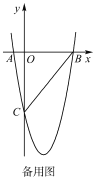
(3)如图，在(2)的条件下，与交于点与交于点，连接，若的面积，求的长.

Answer 1

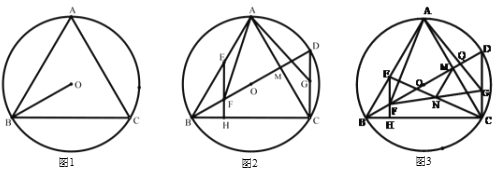
【答案】（1）证明见解析；（2）证明见解析；（3）.

【解析】

（1）连接OA、OC，证明ΔOABΔOBC，根据等边三角形的性质可得AB=BC，又因AB=AC，即可判定ΔABC为等边三角形；（2）过点A作AL⊥CD于L，根据等边三角形的性质可得BD⊥AC，∠ABM=30°，再求得∠ACL=30°，即可判定ΔABMΔACL，由全等三角形的性质可得BM=CL， AM=AL ，再证明RtΔAFMRtΔAGL，即可得FM=GH，由此可得BM-FM=CL-GL，即BF=CG；（3）延长CD至S使得DS=DA，易证ΔADS为等边三角形，即可证得DQAS，由平行线分线段成比例定理可得AQ:QG=SD:DG=5:3，即可得到DA:DG=5:3；设DA=DC=5k,DG=3k，则CG=BF=2k；计算得，所以，；再证明ΔABFΔACG，可得∠BAF=∠CAG，所以∠FAG=∠FAC+∠CAG=∠FAC+∠BAF=60°，即可判定ΔAFG是等边三角形；在中，，解得；由，所以；又因，可得；由(2)知，可判定，可得；再求得，所以等边的面积，解得，所以

(1)证明：连接，

∵，

∴ ， ，

又∵平分，

∴，

∵，

∴，

∴，

又∵，

∴为等边三角形；

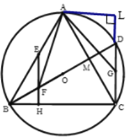
(2)过点作于，

∵平分，

∴ ， ，

∵是直径，

∴，

∴，

∵ ，

∴，

∴， ，

又∵，

∴，

∴，

∴，

即；

(3)延长至使得，

易证为等边，

∵，

∴，

∴，

∴，

设，

则，

计算得，

∴，，

再证明，

∴，

∴，

∴为等边三角形；

在中，

解得

∵

∴

又∵

∴可证

由(2)知

∴

∴

又∵

∴

等边的面积

∴

∴

∴