题目内容
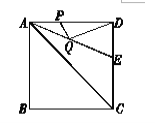
【题目】如图,正方形ABCD的边长是4, ![]() 的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则
的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则![]() 的最小值是( )
的最小值是( )
A. 2 B. 4 C. ![]() D.
D. ![]()
【答案】C
【解析】作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,
∵DD′⊥AE,∴∠AFD=∠AFD′,∵AF=AF,∠DAE=∠CAE,∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=4,∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,∴∠DAD′=45°,∴AP′=P′D′,∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=16,∵AP′=P′D',2P′D′2=AD′2,即2P′D′2=16,
P′D′=![]() ,即DQ+PQ的最小值为
,即DQ+PQ的最小值为![]() ,故选C.
,故选C.

练习册系列答案
相关题目