题目内容
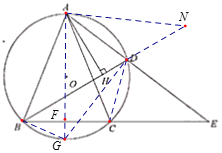
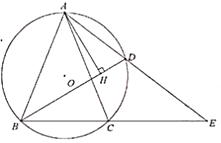
【题目】如图,△ABC内接于⊙O,![]() ,点
,点![]() 为
为![]() 上的动点,且
上的动点,且![]() .
.
(1)求![]() 的长度;
的长度;
(2)在点D运动的过程中,弦AD的延长线交BC的延长线于点E,问ADAE的值是否变化?若不变,请求出ADAE的值;若变化,请说明理由.
(3)在点D的运动过程中,过A点作AH⊥BD,求证:![]() .
.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】(1)过A作AF⊥BC,垂足为F,交⊙O于G,由垂径定理可得BF=1,再根据已知结合RtΔAFB即可求得AB长;
(2)连接DG,则可得AG为⊙O的直径,继而可证明△DAG∽△FAE,根据相似三角形的性质可得ADAE=AFAG,连接BG,求得AF=3,FG=![]() ,继而即可求得ADAE的值;
,继而即可求得ADAE的值;
(3)连接CD,延长BD至点N,使DN=CD,连接AN,通过证明△ADC≌△ADN,可得AC=AN,继而可得AB=AN,再根据AH⊥BN,即可证得BH=HD+CD.
(1)过A作AF⊥BC,垂足为F,交⊙O于G,
∵AB=AC,AF⊥BC,∴BF=CF=![]() BC=1,
BC=1,
在RtΔAFB中,BF=1,∴AB=![]() ;
;
(2)连接DG,
∵AF⊥BC,BF=CF,∴AG为⊙O的直径,∴∠ADG=∠AFE=90°,
又∵∠DAG=∠FAE,∴△DAG∽△FAE,
∴AD:AF=AG:AE,
∴ADAE=AFAG,
连接BG,则∠ABG=90°,∵BF⊥AG,∴BF2=AFFG,
∵AF=![]() =3,
=3,
∴FG=![]() ,
,
∴ADAE=AFAG=AF(AF+FG)=3×![]() =10;
=10;
(3)连接CD,延长BD至点N,使DN=CD,连接AN,
∵∠ADB=∠ACB=∠ABC,∠ADC+∠ABC=180°,∠ADN+∠ADB=180°,
∴∠ADC=∠ADN,
∵AD=AD,CD=ND,
∴△ADC≌△ADN,
∴AC=AN,
∵AB=AC,∴AB=AN,
∵AH⊥BN,
∴BH=HN=HD+CD.