题目内容
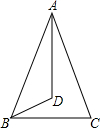如图△ABC中，AB=AC，角平分线AD、BD相交于点D．若∠ABC=80°，则∠ADB等于
- A.100°
- B.110°
- C.120°
- D.130°
D
分析：因为AB=AC，∠ABC=80°，可求出∠C的度数，进而求出∠BAC的度数，根据角平分线的性质，可求出∠BAD和∠DBA的度数，进而求出∠ADB的度数．
解答：∵AB=AC，
∴∠C=∠ABC=80°，
∴∠BAC=180°-∠C-∠ABC=180°-80°-80°=20°
∵AD，BD分别是∠BAC，∠ABC的角平分线，
∴∠BAD=
∠BAC=×20°=10°．
∠ABD=×∠ABC=×80°=40°．
∴∠ADB=180°-10°-40°=130°．
故选D．
点评：本题考查等腰三角形的性质，等腰三角形的两个底角相等以及三角形的内角和为180°，从而可列方程求解．
分析：因为AB=AC，∠ABC=80°，可求出∠C的度数，进而求出∠BAC的度数，根据角平分线的性质，可求出∠BAD和∠DBA的度数，进而求出∠ADB的度数．
解答：∵AB=AC，
∴∠C=∠ABC=80°，
∴∠BAC=180°-∠C-∠ABC=180°-80°-80°=20°
∵AD，BD分别是∠BAC，∠ABC的角平分线，
∴∠BAD=
∠BAC=×20°=10°．∠ABD=
×∠ABC=×80°=40°．∴∠ADB=180°-10°-40°=130°．
故选D．
点评：本题考查等腰三角形的性质，等腰三角形的两个底角相等以及三角形的内角和为180°，从而可列方程求解．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
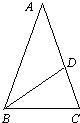13、如图△ABC中，AB=AC，BD平分∠ABC，且△ABC∽△BDC，则∠A=
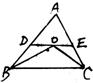8、如图△ABC中，AB=3，AC=2，BO平分∠ABC，CO平分∠ACB．DE过点O交AB于D，交AC于E，且DE∥BC．则△ADE周长为
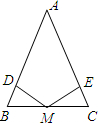如图△ABC中，AB=AC，M是BC中点，D，E分别在AB，AC上，且BD=CE，求证：ME=MD．
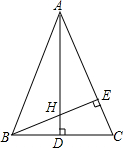已知：如图△ABC中，AB=AC，AD和BE是高，它们交于点H，且AE=BE，
如图△ABC中，AB=6，AC=