题目内容
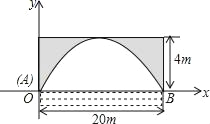
【题目】有一座抛物线形拱桥,正常水位时桥下水面宽为20m,拱顶距水面4m.
(1)在如图的直角坐标系中,求出该抛物线的解析式;
(2)为保证过往船只顺利航行,桥下水面宽度不得小于18m,求水面在正常水位基础上,最多涨多少米,不会影响过往船只?
【答案】(1)y=﹣0.04(x﹣10)2+4(2)0.76m
【解析】
(1)设所求抛物线的解析式为:y=a(x﹣h)2+k,由已知条件易知h和k的值,再把点C的坐标代入求出a的值即可;
(2)由题意得可设E(1,y),把点E的坐标代入已经求出的抛物线解析式求出y的值即可得到最多涨多少米不会影响过往船只.
(1)设所求抛物线的解析式为:y=a(x﹣h)2+k,
∵由AB=20,AB到拱桥顶C的距离为4m,
则C(10,4),A(0,0),B(20,0)
把A,B,C的坐标分别代入得a=﹣0.04,h=10,k=4
抛物线的解析式为y=﹣0.04(x﹣10)2+4;
(2)由题意得可设E(1,y),
把E点坐标代入抛物线的解析式为y=﹣0.04(x﹣10)2+4,
解得:y=﹣0.76,
∴DF=0.76m.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目