题目内容
【题目】在平面直角坐标系中,O是坐标原点,A(2,2),B(4,﹣3),P是x轴上的一点.
(1)若PA+PB的值最小,求P点的坐标;
(2)若∠APO=∠BPO.
①求此时P点的坐标;
②在y轴上是否存在点Q,使得△QAB的面积等于△PAB的面积,若存在,求出Q点坐标;若不存在,说明理由.
【答案】(1)P点坐标为(![]() ,0);(2)①点P坐标为(﹣2,0);②y轴上存在点Q使得△QAB的面积等于△PAB的面积,Q的坐标为(0,﹣5)或(0,19).
,0);(2)①点P坐标为(﹣2,0);②y轴上存在点Q使得△QAB的面积等于△PAB的面积,Q的坐标为(0,﹣5)或(0,19).
【解析】
(1)根据题意画坐标系描点,根据两点之间线段最短,求直线AB解析式,与x轴交点即为所求点P.
(2)①作点A关于x轴的对称点A',根据轴对称性质有∠APO=∠A'PO,所以此时P、A'、B在同一直线上.求直线A'B解析式,与x轴交点即为所求点P.
②法一,根据坐标系里三角形面积等于水平长(右左两顶点的横坐标差)与铅垂高(上下两顶点的纵坐标差)乘积的一半,求得△PAB的面积为12,进而求得△QAP的铅垂高等于6,再得出直线BQ上的点E坐标为(2,8)或(2,﹣4),求出直线BQ,即能求出点Q坐标.法二,根据△QAB与△PAB同以AB为底时,高应相等,所以点Q在平行于直线AB、且与直线AB距离等于P到直线AB距离的直线上.这样的直线有两条,一条即过点P且与AB平行的直线,另一条在AB上方,根据平移距离相等即可求出.所求直线与y轴交点即点Q.
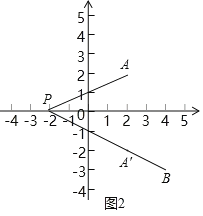
(1)∵两点之间线段最短,∴当A、P、B在同一直线时,PA+PB=AB最短(如图1).
设直线AB的解析式为:y=kx+b.
∵A(2,2),B(4,﹣3),∴![]() ,解得:
,解得: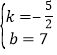 ,∴直线AB:y
,∴直线AB:y![]() x+7.
x+7.
当![]() x+7=0时,得:x
x+7=0时,得:x![]() ,∴P点坐标为(
,∴P点坐标为(![]() ,0).
,0).
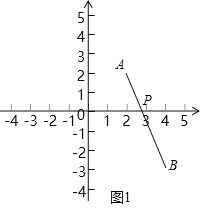
(2)①作点A(2,2)关于x轴的对称点A'(2,﹣2).
根据轴对称性质有∠APO=∠A'PO.
∵∠APO=∠BPO,∴∠A'PO=∠BPO,∴P、A'、B在同一直线上(如图2).
设直线A'B的解析式为:y=k'x+b'.
![]() ,解得:
,解得: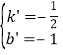 ,∴直线A'B:y
,∴直线A'B:y![]() x﹣1.
x﹣1.
当![]() x﹣1=0时,得:x=﹣2,∴点P坐标为(﹣2,0).
x﹣1=0时,得:x=﹣2,∴点P坐标为(﹣2,0).
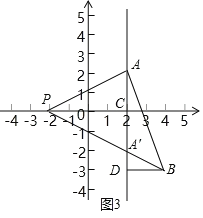
②存在满足条件的点Q.
法一:设直线AA'交x轴于点C,过B作BD⊥直线AA'于点D(如图3),∴PC=4,BD=2,∴S△PAB=S△PAA'+S△BAA'![]() .
.
设BQ与直线AA'(即直线x=2)的交点为E(如图4).
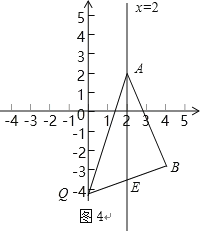
∵S△QAB=S△PAB,则S△QAB![]() 2AE=12,∴AE=6,∴E的坐标为(2,8)或(2,﹣4).
2AE=12,∴AE=6,∴E的坐标为(2,8)或(2,﹣4).
设直线BQ解析式为:y=ax+q.则:
![]() 或
或![]()
解得: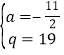 或
或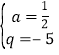 ,∴直线BQ:y
,∴直线BQ:y![]() 或y
或y![]() ,∴Q点坐标为(0,19)或(0,﹣5).
,∴Q点坐标为(0,19)或(0,﹣5).
法二:∵S△QAB=S△PAB,∴△QAB与△PAB以AB为底时,高相等,即点Q到直线AB的距离=点P到直线AB的距离.
i)若点Q在直线AB下方,则PQ∥AB.
设直线PQ:y![]() x+c,把点P(﹣2,0)代入,解得:c=﹣5,y
x+c,把点P(﹣2,0)代入,解得:c=﹣5,y![]() x﹣5,即Q(0,﹣5);
x﹣5,即Q(0,﹣5);
ii)若点Q在直线AB上方.
∵直线y![]() x﹣5向上平移12个单位得直线AB:y
x﹣5向上平移12个单位得直线AB:y![]() x+7,∴把直线AB:y
x+7,∴把直线AB:y![]() x+7再向上平移12个单位得直线AB:y
x+7再向上平移12个单位得直线AB:y![]() x+19,∴Q(0,19).
x+19,∴Q(0,19).
综上所述:y轴上存在点Q使得△QAB的面积等于△PAB的面积,Q的坐标为(0,﹣5)或(0,19).

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案