题目内容
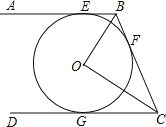
【题目】如图,AB是⊙O的直径,且AB =6,C是⊙O上一点,D是![]() 的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.

(l)求证:AF⊥EF;
(2)填空:
①当BE= 时,点C是AF的中点;
②当BE= 时,四边形OBDC是菱形,
【答案】(1)证明见解析;(2)①6,②3
【解析】试题分析:(1)连结OD,由直线EF与 O相切于点D,得到OD⊥EF,由同圆的半径相等推出∠1=∠3,由点D为![]() 的中点,得到∠1=∠2,证得∠2=∠3,得到OD∥AF,得出结论AF⊥EF;(2)①根据平行线分线段成比例定理,当B为的AE中点时,点C是AF的中点;②由切线的性质可证得OD⊥EF,根据直角三角形斜边上的中线的性质得到BD=OB=BE,
的中点,得到∠1=∠2,证得∠2=∠3,得到OD∥AF,得出结论AF⊥EF;(2)①根据平行线分线段成比例定理,当B为的AE中点时,点C是AF的中点;②由切线的性质可证得OD⊥EF,根据直角三角形斜边上的中线的性质得到BD=OB=BE,
由D是![]() 的中点,得到CD=BD, 由此CD=BD=BO=OD,
的中点,得到CD=BD, 由此CD=BD=BO=OD,
试题解析:
(1)证明:连结OD,
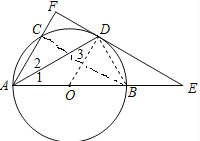
∵直线EF与O相切于点D,
∴OD⊥EF,
∵OA=OD,
∴∠1=∠3,
∵点D为BC的中点,
∴∠1=∠2,
∴∠2=∠3,
∴OD∥AF,
∴AF⊥EF;
(2) ①当BE=6时,
由(1)知,BC∥EF,当AB=BE ,AC=CF,
∴BE=6时,点C是AF的中点,
故答案为:6;
②当BE=3时,
∵AB是⊙O的直径,AB=6,
∴OB=OD=OC=BE=3,
∵ED是⊙O的切线,
∴OD⊥EF,
∴BD=OB=BE,
D是![]() 的中点,
的中点,
∴CD=BD,
∴CD=BD=BO=OD,
四边形OBDC是菱形.
故答案为:3.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目