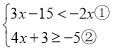题目内容
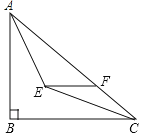
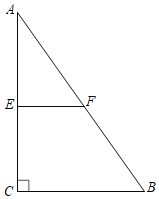
【题目】四边形ABCD为菱形,点E在边AD上,点F在边CD上
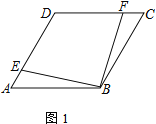
(1) 若AE=CF,求证:EB=BF
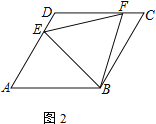
(2) 若AD=4,DE=CF,且△EFB为等边三角形,求四边形DEBF的面积
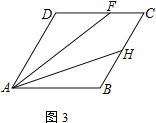
(3) 若∠DAB=60°,点H在边BC上,且BH=HC=2.若∠DFA=2∠HAB,直接写出CF的长
【答案】(1)见解析;(2)S四边形DEBF=![]() ;(3)
;(3)![]() ;
;
【解析】
(1)因为四边形ABCD为菱形,得出AB=BC,∠EAB=∠FBC,又由AE=CF,得出△ABE≌△BCF(SAS),进而得出EB=BF.
(2)连接BD,截取AH=CF,由(1)中得知,△ABE≌△BCF(SAS),得出BH=BF=BE,进而可知∠BHE=∠BEH,∠AHB=∠BED,从而可判定△DEB≌△AHB,得出AB=BD,可判定△DEB≌△CFB,进而得出四边形DEBF的面积等于菱形ABCD面积减去三角形ABD面积,即为三角形ABD的面积,即可得解.
(3)延长AD,作FM⊥AM,交于M,延长DC、AH交于点K,由∠DFA=2∠HAB=∠FAK+∠HAB,可得出∠FAK=∠HAB=∠FKA,进而得出AF=FK,因此DF=4-CF,DM=2-![]() CF,MF=
CF,MF=![]() (4-CF),进而得出AM=4+2-
(4-CF),进而得出AM=4+2-![]() CF=6-
CF=6-![]() CF,根据勾股定理,
CF,根据勾股定理,![]()
进而得出关于CF的方程,即可求出CF.
(1) 证明:∵四边形ABCD为菱形,
∴AB=BC,∠EAB=∠FBC,
又∵AE=CF,
∴△ABE≌△BCF(SAS)
∴EB=BF.
(2)如图所示,连接BD,截取AH=CF
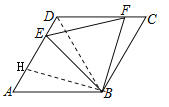
由(1)中得知,△ABE≌△BCF(SAS)
∴BH=BF=BE
∴∠BHE=∠BEH
∴∠AHB=∠BED
∴△DEB≌△AHB,
∴AB=BD
∴△DEB≌△CFB,
∴四边形DEBF的面积等于菱形ABCD面积减去三角形ABD面积,即为三角形ABD的面积,
S四边形DEBF=![]() =
=![]()
(3)如图所示,延长AD,作FM⊥AM,交于M,延长DC、AH交于点K,
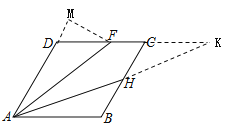
∵∠DFA=2∠HAB=∠FAK+∠HAB
∴∠FAK=∠HAB=∠FKA
∴AF=FK
∴DF=4-CF,DM=2-![]() CF,MF=
CF,MF=![]() (4-CF),
(4-CF),
∴AM=4+2-![]() CF=6-
CF=6-![]() CF
CF
又![]()
![]()
∴CF=![]()

 阅读快车系列答案
阅读快车系列答案