题目内容
19.某商店第一次用3000元购进某款书包,很快卖完,第二次又用2400元购进该款书包,但这次每个书包的进价是第一次进价的1.2倍,数量比第一次少了20个.(1)设第一次书包的进价为x元/个,则第二次的进价为1.2x元/个;设第一次购进书包y个,则第二次购进书包(y-20)个.(直接写答案)
(2)根据(1)设的未知数,列方程组并解答:第一次每个书包的进价是多少元?
(3)在第二次的销售过程中,若按80/个的价格销售,恰好销售完一半时,根据市场情况,商店决定对剩余的书包全部按同一标准一次性打折销售,但要求利润不少于480元,问最低可打几折?
分析 (1)根据信息“第一次每个书包的进价是x元,但这次每个书包的进价是第一次进价的1.2倍,数量比第一次少了20个”填空.
(2)设最低可以打x折,根据若第二次进货后按80元/个的价格销售,恰好销售完一半时,根据市场情况,商店决定对剩余的书包全部按同一标准一次性打折销售,但要求这次的利润不少于480元,可列出不等式求解.
解答 解:(1)设第一次书包的进价为x元/个,则第二次的进价为 1.2x元/个;设第一次购进书包y个,则第二次购进书包 (y-20)个.(直接写答案)
故答案是:1.2x;(y-20);
(2)设第一次每个书包的进价是x元,
$\frac{3000}{x}$-20=$\frac{2400}{1.2x}$,
x=50.
经检验得出x=50是原方程的解,且符合题意,
即:第一次书包的进价是50元.
设最低可以打z折.
2400÷(50×1.2)=40
80×20+80×0.1z•20-2400≥480
y≥8
故最低打8折.
点评 本题考查理解题意能力,第一问以数量做为等量关系列方程求解,第二问以利润做为不等量关系列不等式求解.

练习册系列答案
相关题目
7.下列说法不正确的是( )
| A. | 0既不是正数,也不是负数 | B. | -0.5是负分数 | ||
| C. | 一个有理数不是整数就是分数 | D. | -1是负数,但不是整数 |
14.龙东东同学家买了一辆轿车,他连续10天记录了他家轿车每天行驶的路程,以40km为标准,超过或不足的分别用正数、负数来表示,得到的数据分别如下(单位:km):
(1)请你运用所学知识算一算龙东东家轿车这十天行驶的路程;
(2)若已知轿车每行驶100km耗用汽油7升,且汽油的价格为每升7.20元,请你根据第(1)题估计龙东东家轿车一个月(按30天计算)的汽油费用.
| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | 第八天 | 第九天 | 第十天 | |
| 路程 (km) | +2 | -4 | +5 | -3 | +2 | +3 | +1 | -2 | +4 | -8 |
(2)若已知轿车每行驶100km耗用汽油7升,且汽油的价格为每升7.20元,请你根据第(1)题估计龙东东家轿车一个月(按30天计算)的汽油费用.
4.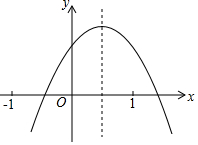 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论 ①a+b+c<0②a-b+c<0③b+2a<0④abc>0(5)b2<4ac,其中正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论 ①a+b+c<0②a-b+c<0③b+2a<0④abc>0(5)b2<4ac,其中正确的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论 ①a+b+c<0②a-b+c<0③b+2a<0④abc>0(5)b2<4ac,其中正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论 ①a+b+c<0②a-b+c<0③b+2a<0④abc>0(5)b2<4ac,其中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.|a|=3,|b|=1,且a>b,那么a+b的值为( )
| A. | 4 | B. | 2或-4 | C. | -4 | D. | 4或2 |
 如图,四边形ABCD是正方形,AE=4cm,BE=2cm,对角线AC上一点P,使PE+PB的值最小,则PE+PB的最小值=2$\sqrt{13}$cm.
如图,四边形ABCD是正方形,AE=4cm,BE=2cm,对角线AC上一点P,使PE+PB的值最小,则PE+PB的最小值=2$\sqrt{13}$cm.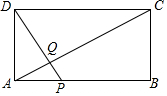 如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.