题目内容
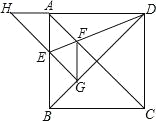
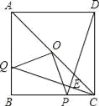
【题目】如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP⊥CQ于点E,交BC于点P,连接OP,OQ;
求证:(1)△BCQ≌△CDP;(2)OP=OQ.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据正方形的性质和DP⊥CQ于点E可以得到证明△BCQ≌△CDP的全等条件;
(2)根据(1)得到BQ=PC,然后连接OB,根据正方形的性质可以得到证明△BOQ≌△COP的全等条件,然后利用全等三角形的性质就可以解决题目的问题.
证明:(1)∵四边形ABCD是正方形,
∴∠B=∠PCD=90°,BC=CD,
∴∠2+∠3=90°,
又∵DP⊥CQ,
∴∠2+∠1=90°,
∴∠1=∠3,
在△BCQ和△CDP中,
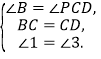
∴△BCQ≌△CDP;
(2)连接OB,
由(1)△BCQ≌△CDP可知:BQ=PC,
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∵点O是AC中点,
∴BO=![]() AC=CO,∠4=
AC=CO,∠4=![]() ∠ABC=45°=∠PCO,
∠ABC=45°=∠PCO,
在△BOQ和△COP中,
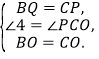
∴△BOQ≌△COP,
∴OQ=OP.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目