题目内容
如图,已知二次函数 的图像经过点A(-3,-1)和点B(-3,-9).
的图像经过点A(-3,-1)和点B(-3,-9).

(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,-m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
 的图像经过点A(-3,-1)和点B(-3,-9).
的图像经过点A(-3,-1)和点B(-3,-9).
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,-m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
(1)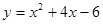 (2)对称轴为
(2)对称轴为 ;顶点坐标为(-2,-10)(3) m=1,1
;顶点坐标为(-2,-10)(3) m=1,1
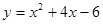 (2)对称轴为
(2)对称轴为 ;顶点坐标为(-2,-10)(3) m=1,1
;顶点坐标为(-2,-10)(3) m=1,1解:(1)将x=1,y=-1;x=-3,y=-9分别代入 得
得
 解得
解得 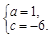 …………………………(3分)
…………………………(3分)
∴二次函数的表达式为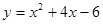 . ………………………………(4分)
. ………………………………(4分)
(2)对称轴为 ;顶点坐标为(-2,-10). ………………………………(6分)
;顶点坐标为(-2,-10). ………………………………(6分)
(3)将(m,-m)代入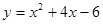 ,得
,得 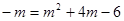 ,
,
解得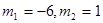 .∵m>0,∴
.∵m>0,∴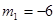 不合题意,舍去.
不合题意,舍去.
∴ m=1. …………………………………………………………………(7分)
∵点P与点Q关于对称轴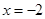 对称,
对称,
∴点Q到x轴的距离为1. ………………………………………………(8分)
(1)用待定系数法(将图像上两点坐标代入解析式即可)
(2)对称轴为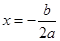 ,顶点坐标为
,顶点坐标为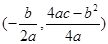
(3)将点P代入二次函数解析式求出m的值,由于点P和点Q 关于抛物线的对称轴对称,故它们到到x轴的距离也相等,距离为1.
 得
得 解得
解得 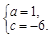 …………………………(3分)
…………………………(3分)∴二次函数的表达式为
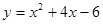 . ………………………………(4分)
. ………………………………(4分)(2)对称轴为
 ;顶点坐标为(-2,-10). ………………………………(6分)
;顶点坐标为(-2,-10). ………………………………(6分)(3)将(m,-m)代入
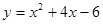 ,得
,得 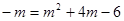 ,
,解得
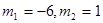 .∵m>0,∴
.∵m>0,∴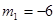 不合题意,舍去.
不合题意,舍去.∴ m=1. …………………………………………………………………(7分)
∵点P与点Q关于对称轴
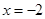 对称,
对称,∴点Q到x轴的距离为1. ………………………………………………(8分)
(1)用待定系数法(将图像上两点坐标代入解析式即可)
(2)对称轴为
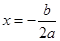 ,顶点坐标为
,顶点坐标为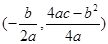
(3)将点P代入二次函数解析式求出m的值,由于点P和点Q 关于抛物线的对称轴对称,故它们到到x轴的距离也相等,距离为1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
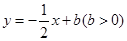 分别交
分别交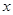 轴,
轴,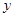 轴于
轴于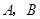 两点,以
两点,以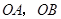 为边作矩形
为边作矩形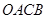 ,
,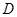 为
为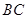 的中点.以
的中点.以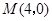 ,
,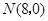 为斜边端点作等腰直角三角形
为斜边端点作等腰直角三角形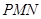 ,点
,点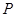 在第一象限,设矩形
在第一象限,设矩形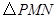 重叠部分的面积为
重叠部分的面积为 .
.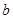 值由小到大变化时,求
值由小到大变化时,求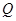 ,使
,使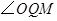 等于
等于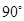 ,求出
,求出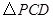 为等腰三角形,请直接写出所有符合条件的
为等腰三角形,请直接写出所有符合条件的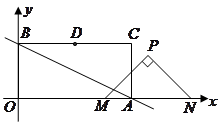
 的图像与
的图像与 轴相交于点A、B,顶点为C,点D在这个二次函数图像的对称轴上,若四边形ABCD时一个边长为2且有一个内角为60°的菱形,求此二次函数的表达式。
轴相交于点A、B,顶点为C,点D在这个二次函数图像的对称轴上,若四边形ABCD时一个边长为2且有一个内角为60°的菱形,求此二次函数的表达式。
 的图象如图所示,则其对称轴是 ,当函数值
的图象如图所示,则其对称轴是 ,当函数值 时,对应
时,对应 的取值范围是 .
的取值范围是 .
