题目内容
小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x(单位：cm)的边与这条边上的高之和为40 cm，这个三角形的面积S(单位：cm2)随x(单位：cm)的变化而变化．
（1）请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；
（2）当x是多少时，这个三角形面积S最大?最大面积是多少?
（1）请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；
（2）当x是多少时，这个三角形面积S最大?最大面积是多少?
（1）S=
（2）当x为20cm时，三角形最大面积是200cm2
（2）当x为20cm时，三角形最大面积是200cm2解：（1）S=。
（2）∵a=
＜0，∴S有最大值。
∴当
时，
。
∴当x为20cm时，三角形最大面积是200cm2。
（1）由长度为x的边与这条边上的高之和为40 可得x边上的高=40－x。
由三角形面积公式得S=
x·（40－x），化简即可。
（2）根据（1）的关系式，利用公式法求得二次函数的最值即可。
。（2）∵a=
＜0，∴S有最大值。∴当
时，。∴当x为20cm时，三角形最大面积是200cm2。
（1）由长度为x的边与这条边上的高之和为40 可得x边上的高=40－x。
由三角形面积公式得S=
x·（40－x），化简即可。（2）根据（1）的关系式，利用公式法求得二次函数的最值即可。
练习册系列答案
相关题目
与它的对称轴相交于点
，与
轴交于
，与
轴正半轴交于
．
交
是线段
上一动点（
点异于
），过
轴交直线
于
，过
轴于
，求当四边形
的面积等于
时点
的图像经过点A(-3,-1)和点B(-3,-9)．
（单位：米）与小球运动时间
（单位：秒）的函数关系式是
，那么小球运动中的最大高度
．
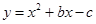的图象经过点
，则
的值为 ．