题目内容
如图,⊙O的直径AB=6cm,P是AB延长线上的一点,过点P作⊙O的切线,切点为C,连接AC,BC.

(1)若∠CPA=30°,求PC的长;
(2)探究:当点P在AB的延长线上运动时,是否总存在∠PCB=∠CAB?若存在,请证明;若不存在,请说明理由.

(1)若∠CPA=30°,求PC的长;
(2)探究:当点P在AB的延长线上运动时,是否总存在∠PCB=∠CAB?若存在,请证明;若不存在,请说明理由.
(1)PC= cm;(2)存在,理由详见解析.
cm;(2)存在,理由详见解析.
 cm;(2)存在,理由详见解析.
cm;(2)存在,理由详见解析.试题分析:(1)连接OC,由切线的性质得OC⊥PC,然后根据三角函数定义可求PC的值;(2)由切线的性质得∠OCB+∠PCB=90°,因为AB是圆的直径,根据“直径所对的圆周角是直角”得∠A+∠ABC=90°,根据等角的余角相等,可知∠PCB=∠CAB.归纳:连接圆心与切点之间的半径是常见的辅助线.
试题解析:(1)连接OC,
∵PC为⊙O的切线,
∴OC⊥PC,∴∠PCO=90°,
∴在Rt△PCO中,tan∠CPA=
 ,
,又∠CPA=30°,AB=6cm,
∴
 (cm),
(cm),(2)存在.证明如下:
∵PC为⊙O的切线,
∴∠PCO=∠OCB+∠PCB=90°
又∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠CAB+∠ABC=90°,
∴∠PCB+∠OCB=∠CAB+∠ABC=90°
又∵OB=OC,
∴∠OCB=∠ABC,
∴∠PCB=∠CAB.


练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
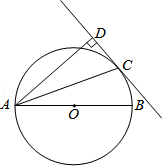
 ,求⊙O的半径长.
,求⊙O的半径长. ∠CAB.
∠CAB.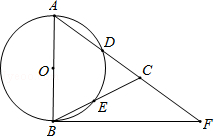
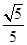 ,求BC和BF的长.
,求BC和BF的长.
 ,求⊙O的半径。
,求⊙O的半径。

 cm
cm
 cm
cm cm
cm