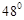题目内容
如图,AB是⊙O的弦,D是半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于F,且CE=CB。

(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;(3)如果CD=15,BE=10,sinA= ,求⊙O的半径。
,求⊙O的半径。

(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;(3)如果CD=15,BE=10,sinA=
 ,求⊙O的半径。
,求⊙O的半径。(1)见解析;(2)30 °(3) .
.
 .
.试题分析:(1)连接OB,有圆的半径相等和已知条件证明∠OBC=90°即可证明BC是⊙O的切线;
(2)连接OF,AF,BF,首先证明△OAF是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠ABF的度数;
(3)过点C作CG⊥BE于点G,由CE=CB,可求出EG=
 BE=5,又Rt△ADE∽Rt△CGE和勾股定理求出DE=2,由Rt△ADE∽Rt△CGE求出AD的长,进而求出⊙O的半径.
BE=5,又Rt△ADE∽Rt△CGE和勾股定理求出DE=2,由Rt△ADE∽Rt△CGE求出AD的长,进而求出⊙O的半径.试题解析:
(1)证明:连接OB
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC
又∵CD⊥OA
∴∠A+∠AED=∠A+∠CEB="90" °
∴∠OBA+∠ABC="90" °
∴OB⊥BC
∴BC是⊙O的切线.

(2)连接OF,AF,BF,
∵DA=DO,CD⊥OA,
∴△OAF是等边三角形,
∴∠AOF="60" °
∴∠ABF=
 ∠AOF="30" °
∠AOF="30" °
(3)过点C作CG⊥BE于点G,由CE=CB,
∴EG=
 BE=5
BE=5又Rt△ADE∽Rt△CGE
∴sin∠ECG=sin∠A=
 ,
,∴CE=
 =13
=13∴CG=
 =12,
=12,又CD=15,CE=13,
∴DE=2,
由Rt△ADE∽Rt△CGE得

∴AD=
 =
=
∴⊙O的半径为2AD=
 .
.

练习册系列答案
相关题目



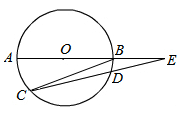
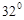 B.
B.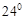 C.
C. D.
D.