Question

【题目】如图，点A是直线y=﹣x上的动点，点B是x轴上的动点，若AB=2，则△AOB面积的最大值为（　　）

A. 2 B. +1 C. -1 D. 2

Answer 1

【答案】B

【解析】

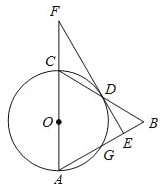
作△AOB的外接圆⊙C，连接CB，CA，CO，过C作CD⊥AB于D，则CA=AB，连接OD，则OD≤OC+CD，依据当O，C，D在同一直线上时，OD的最大值为OC+CD=+1，即可得到△AOB的面积最大值．

解：如图所示，

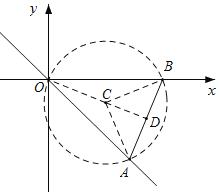
作△AOB的外接圆⊙C，连接CB，CA，CO，过C作CD⊥AB于D，则CA=AB，

由题可得∠AOB=45°，

∴∠ACB=90°，

∴CD=AB=1，AC=BC==CO，

连接OD，则OD≤OC+CD，

∴当O，C，D在同一直线上时，OD的最大值为OC+CD=+1，

此时OD⊥AB，

∴△AOB的面积最大值为AB×OD=×2（+1）=+1，

当点A在第二象限内，点B在x轴负半轴上时，

同理可得，△AOB面积的最大值为+1，

故选：B．