题目内容
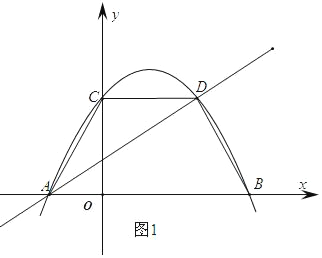
【题目】如图,平面直角坐标系中,直线l:y=![]() x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
(1)求点A的坐标;
(2)求此二次函数的解析式;
(3)点P为直线l上一动点,将线段AC绕点P顺时针旋转α°(0°<α°<360°)得到线段A'C'(点A,A'是对应点,点C,C'是对应点).请问:是否存在这样的点P,使得旋转后点A'和点C'分别落在直线l和抛物线y=ax2﹣3ax+c的图象上?若存在,请直接写出点A'的坐标;若不存在,请说明理由.
【答案】(1) A(﹣1,0);(2) y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2;(3)见解析.
x+2;(3)见解析.
【解析】
(1)由题意可得C(0,c),且CD∥x轴,可得D(3,c),根据面积比可得AB=5.由对称性可得点A(-2m,0)到对称轴的距离2倍是5,可求m,即可求A点坐标.
(2)由直线l过D点可求D(3,2),由A,B关于对称轴对称可求B(4,0),则可用交点式求二次函数的解析式.
(3)由点A是直线l上一点,绕直线l上点P旋转,且落在直线l上,因此可得点A与点A'重合,或点A绕点P旋转180°得到A'.设C'(a,-![]() a2+
a2+![]() a+2)根据中点坐标公式可求A'点坐标.
a+2)根据中点坐标公式可求A'点坐标.
解:(1)
∵二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点
∴C(0,c,),对称轴是直线x=![]() =
=![]() .
.
∵CD∥x轴.
∴C,D关于对称轴直线x=![]() 对称.
对称.
∴D(3,c).
∵S△ACD:S△ABD=3:5.且△ACD和△ABD是等高的.
∴![]() .
.
∴AB=5.
∵直线y=![]() x+m与x轴交于A点,
x+m与x轴交于A点,
∴A(﹣2m,0).
∵点A,点B关于对称轴x=![]() 对称.
对称.
∴2×[![]() ﹣(﹣2m)]=5.
﹣(﹣2m)]=5.
∴m=![]() .
.
∴A(﹣1,0),且AB=5.
∴B(4,0).
(2)设抛物线解析式y=a(x+1)(x﹣4).
∵m=![]() .
.
∴直线AD解析式y=![]() x+
x+![]() .
.
∵D(3,c)在直线AD上.
∴c=![]() +
+![]() =2.
=2.
∴D(3,2)且在抛物线上.
∴2=a(3+1)(3﹣4).
∴a=﹣![]() .
.
∴抛物线解析式y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2.
x+2.
(3)∵点A在直线l上,旋转后A'点落在直线l上,
∴点A与点A'重合,或者点A绕着点P旋转180°.
当点A与点A'重合时,A'(﹣1,0).
当点A绕着点P旋转180°得到A',点C绕着点P旋转180°得到C'
∴AP=A'P,CP=CP'.
如图2:
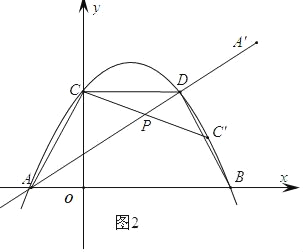
设C'(a,﹣![]() a2+
a2+![]() a+2).
a+2).
∵C( 0,2),CP=CP'.
∴P(![]() a,﹣
a,﹣![]() a2+
a2+![]() a+2).
a+2).
∵点P在直线l上,
∴﹣![]() a2+
a2+![]() a+2=
a+2=![]() a+
a+![]() .
.
即 a2﹣2a﹣6=0.
解得:a1=1+![]() ,a2=1﹣
,a2=1﹣![]() .
.
当a1=1+![]() 时,y=
时,y=![]() ×
×![]() (1+
(1+![]() )+
)+![]() =
=![]() .
.
∴P(![]() ,
,![]() ).
).
∵AP=A'P.
∴A'(2+![]() ,
,![]() ).
).
当a2=1﹣![]() 时,y=
时,y=![]() ×
×![]() (1﹣
(1﹣![]() )+
)+![]() =
=![]() .
.
∴P(![]() ,
,![]() ).
).
∵AP=AP'.
∴A'(2﹣![]() ,
,![]() ).
).
综上所述A'(2﹣![]() ,
,![]() ),(2+
),(2+![]() ,
,![]() ),(﹣1,0).
),(﹣1,0).

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案