题目内容
【题目】如图是小明利用等腰直角三角板测量旗杆高度的示意图.等腰直角三角板的斜边BD与地面AF平行,当小明的视线恰好沿BC经过旗杆顶部点E时,测量出此时他所在的位置点A与旗杆底部点F的距离为10米.如果小明的眼睛距离地面1.7米,那么旗杆EF的高度为( )

A. 10米 B. 11.7米 C. 10![]() 米 D. (5
米 D. (5![]() +1.7)米
+1.7)米
【答案】B
【解析】
延长BD交EF于H,如图,利用四边形ABHF为矩形得到AF=BH=10,HF=AB=1.7,再利用△BCD为等腰直角三角形,可判断△BHE为等腰直角三角形,所以EH=BH=10,然后计算EH+HF即可.
延长BD交EF于H,如图,
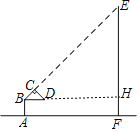
∵BD∥AF,EF⊥AF,
∴BH⊥EF,
易得四边形ABHF为矩形,
∴AF=BH=10,HF=AB=1.7,
∵△BCD为等腰直角三角形,
∴∠CBD=45°,
∴△BHE为等腰直角三角形,
∴EH=BH=10,
∴EF=EH+HF=10+1.7=11.7.
答:旗杆EF的高度为11.7m.
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目







