Question

【题目】如图，点F，G分别在△ADE的AD，DE边上，C，B依次为GF延长线上两点，AB=AD，∠BAF=∠CAE，∠B=∠D．

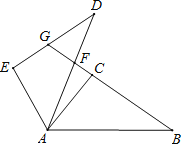
（1）求证：BC=DE；

（2）若∠B=35°，∠AFB=78°，直接写出∠DGB的度数．

Answer 1

【答案】（1）见解析；（2）67°．

【解析】

试题分析：（1）由∠BAF=∠CAE，等式两边同时减去∠CAF，可得出∠BAC=∠DAE，再由AB=AD，∠B=∠D，理由ASA得出△ABC≌△ADE，利用全等三角形的对应边相等可得证；

（2）由∠B=∠D，以及一对对顶角相等，利用两对对应角相等的两三角形相似得到三角形ABF与三角形DGF相似，由相似三角形的对应角相等得到∠DGB=∠BAD，在三角形AFB中，由∠B及∠AFB的度数，利用三角形的内角和定理求出∠BAD的度数，进而得到∠DGB的度数．

（1）证明：∵∠BAF=∠CAE，

∴∠BAF﹣∠CAF=∠CAE﹣∠CAF，

∴∠BAC=∠DAE，

在△ABC和△ADE中，

，

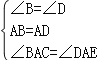∴△ABC≌△ADE（ASA），

∴BC=DE；

（2）解：∠DGB的度数为67°，理由为：

∵∠B=∠D，∠AFB=∠GFD，

∴△ABF∽△GDF，

∴∠DGB=∠BAD，

在△AFB中，∠B=35°，∠AFB=78°，

∴∠DGB=∠BAD=180°﹣35°﹣78°=67°．