��Ŀ����
����Ŀ���ƽ�ָ�����ϸ�ı����ԡ������ԡ���г�ԣ��̲��ŷḻ����ѧ��ֵ���ƽ�ָ���ָ������һ��Ϊ�����ϴ������岿�ֵı�ֵ���ڽ�С������ϴֵı�ֵ�����ֵԼΪ0.618�������ֵ������Ϊ�ƽ�ָ������ҹ�������ѧ�һ����ռ���������Ҫ������ѡ������һ��0.618��ҲӦ���˻ƽ�ָ�����
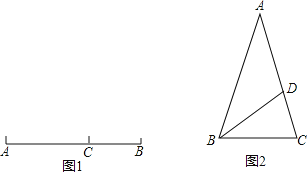
���壺��C���߶�AB�ϣ�������AC2=BCAB����Ƶ�CΪ�߶�AB�Ļƽ�ָ��(��ͼ1).
��ͼ2����ABC�У�AB=AC=1����A=36����BDƽ�֡�ABC��AC�ڵ�D��
(1)��֤����D���߶�AC�Ļƽ�ָ�㣻
��2������߶�AD�ij���
���𰸡���1�������������2��![]()
��������������������ڣ�1�������������Ƴ�ͼ�ж�����ȵĽǣ���������BCD�ס�ACB���������������ε����ʵõ���Ӧ�߳ɱ�����
ͨ�������ɵ�ͼ�ж���ǵĶ�����������BC=BD��BD=AD�������õ�BC=AD�����ûƽ�ָ��Ķ���֤�ý��ۣ�
���ڣ�2�������ݻƽ�ָ��Ķ����֪AD2=ACCD����CD��Ϊ��AC��AD�����ٽ���֪AC=1�����ʽ���AD�ij���.
�⣺��1���ߡ�A=36�㣬AB=AC�����ABC=��ACB=72�㡣
��BDƽ�֡�ABC�����CBD=��ABD=36�㣬��BDC=72�㡣
��AD=BD��BC=BD��
���ABC�ס�BDC��
��![]() ����
����![]() ��
��
��AD2=ACCD��
���D���߶�AC�Ļƽ�ָ�㡣
��2���ɣ�1��AD2=ACCD��
��AD2=AC��AC��AD����AD2=1��AD��AD2+AD��1=0��
���AD=![]() ����ȥ��ֵ����
����ȥ��ֵ����
��AD=![]() ��
��