题目内容
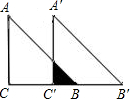 如图,已知Rt△ABC中,∠C=90°,BC=7,AC=7,现将△ABC沿CB方向平移到△A′B′C′的位置.
如图,已知Rt△ABC中,∠C=90°,BC=7,AC=7,现将△ABC沿CB方向平移到△A′B′C′的位置.(1)若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积;
(2)若平移距离为x(x<7),且△ABC与△A′B′C′的重叠部分的面积y,请写出y与x的关系式?
分析:(1)由于AC=BC=7,则△ACB是等腰直角三角形,那么阴影部分也应是等腰三角形,欲求其面积,需求出直角边BC′的长,已知平移的距离为3,即CC′=3,则BC′=7-3=4,根据等腰三角形的面积计算方法即可求出阴影部分(即△ABC与△A′B′C′的重叠部分)的面积.
(2)思路和解法同(1).
(2)思路和解法同(1).
解答:解:(1)∵△A′B′C′由△ABC平移而得到,
∴AC∥A′C′,∴∠ACB=∠A′C′B′=90°,
∵∠ABC=45°,
∴阴影部分三角形为等腰三角形.
∵BC′=CB-CC′=7-3=4,
∴阴影部分的面积S=
×42=8.(6分)
(2)同理,y=
(7-x)2.(10分)
∴AC∥A′C′,∴∠ACB=∠A′C′B′=90°,
∵∠ABC=45°,
∴阴影部分三角形为等腰三角形.
∵BC′=CB-CC′=7-3=4,
∴阴影部分的面积S=
| 1 |
| 2 |
(2)同理,y=
| 1 |
| 2 |
点评:此题主要考查了三角形面积的求法以及根据实际问题列二次函数关系式,此题的关键在于发现阴影部分是个等腰直角三角形.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.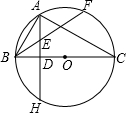 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为