��Ŀ����
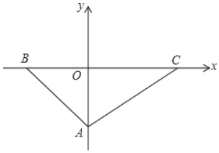
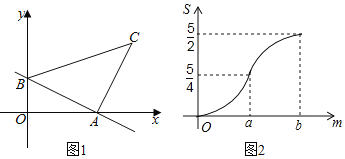
����Ŀ����ͼ1��ֱ��AB��x�ᡢy��ֱ��ཻ�ڵ�A��B�����߶�AB�Ƶ�A˳ʱ����ת90�����õ�AC������BC������ABC������BAƽ�ƣ�����C����x��ʱ�˶�ֹͣ����ƽ�ƾ���Ϊm��ƽ�ƺ��ͼ����x���·����ֵ����ΪS��S����m�ĺ���ͼ����ͼ2��ʾ������0��m��a��a��m��bʱ�������Ľ���ʽ��ͬ����
��1����գ���ABC�����Ϊ ��
��2����ֱ��AB�Ľ���ʽ��
��3����S����m�Ľ���ʽ����д��m��ȡֵ��Χ��
���𰸡���1��![]() ����2��ֱ��AB�Ľ���ʽΪy=��
����2��ֱ��AB�Ľ���ʽΪy=��![]() x+1����3��S=
x+1����3��S=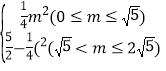 ��
��
����������1����ͼ2���ƽ�Ƽ��ɵó����ۣ�
��2���жϳ���AOB�ա�CEA���ó�AE��OB��CE��OA������ͼ2֪����C���������ǵ�B�������2������������������ABC��������OB��OA�����ɵó����ۣ�
��3����������������������ε������ʽ�������ε������ɵó����ۣ�
��1�������ABC���ƶ���ͼ2֪����B�ƶ�����A��������ͼ2�У�m=aʱ��S=S��A'B'D=![]() ����C�ƶ���x����ʱ������m=bʱ��S=S��A'B'C'=S��ABC=
����C�ƶ���x����ʱ������m=bʱ��S=S��A'B'C'=S��ABC=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����ͼ2������C��CE��x����E��
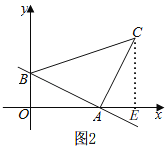
���AEC=��BOA=90�㣮
�ߡ�BAC=90�㣬
���OAB+��CAE=90�㣬
�ߡ�OAB+��OBA=90�㣬
���OBA=��CAE��
����ת֪��AB=AC��
����AOB�ա�CEA��
��AE=OB��CE=OA��
��ͼ2֪����C���������ǵ�B�������2����
��OA=2OB��
��AB2=5OB2��
�ɣ�1��֪��S��ABC=![]() =
=![]() AB2=
AB2=![]() ��5OB2��
��5OB2��
��OB=1��
��OA=2��
��A��2��0����B��0��1����
��ֱ��AB�Ľ���ʽΪy=��![]() x+1��
x+1��
��3���ɣ�2��֪��AB2=5��
��AB=![]() ��
��
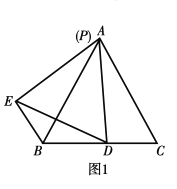
�ٵ�0��m��![]() ʱ����ͼ3��
ʱ����ͼ3��
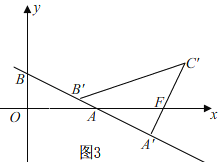
�ߡ�AOB=��AA'F����OAB=��A'AF��
����AOB�ס�AA'F��
��![]() ��
��
���˶�֪��AA'=m����![]() ��
��
��A'F=![]() m��
m��
��S=![]() AA'��A'F=
AA'��A'F=![]() m2��
m2��
�ڵ�![]() ��m��2
��m��2![]() ʱ����ͼ4��
ʱ����ͼ4��
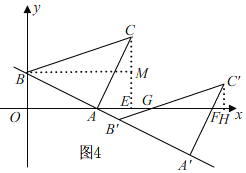
ͬ�ٵķ����ã�A'F=![]() m��
m��
��C'F=![]() ��
��![]() m��
m��
����C��CE��x����E������B��BM��CE��E��
��BM=3��CM=1��
��֪����ACE�ס�FC'H��
��![]() ��
��
��![]() ��
��
��C'H=![]() ��
��
��Rt��FHC'��FH=![]() C'H=
C'H=![]() ��
��
��ƽ��֪����C'GF=��CBM��
�ߡ�BMC=��GHC'��
����BMC�ס�GHC'��
��![]() ��
��
��![]() ��
��
��GH=![]() ��
��
��GF=GH��FH=![]() ��
��
��S=S��A'B'C'��S��C'FG=![]() ��
��![]() ��
��![]() ��
��![]() =
=![]() ��
��![]() ��2
��2![]() ��m��2��
��m��2��
����S=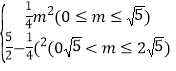 ��
��