题目内容
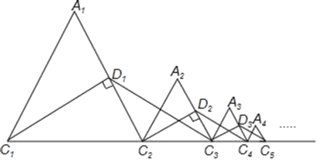
【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnnCn+1的周长和为_____.(n≥2,且n为整数)
【答案】![]() .
.
【解析】
根据等边三角形的性质分别求出△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长即可解决问题.
解:∵等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,
∴A1D1=D1C2,
∴△A2C2C3的周长=![]() △A1C1C2的周长=
△A1C1C2的周长=![]() ,
,
∴△A1C1C2,△A2C2C3,△A3C3C4,…,△AnnCn+1的周长分别为1,![]() ,
,![]() ,…,
,…,![]() ,
,
∴△A1C1C2,△A2C2C3,△A3C3C4,…,△AnnCn+1的周长和为1+![]() +
+![]() +…+
+…+![]() =
=![]() .
.
故答案为: ![]() .
.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
【题目】小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.
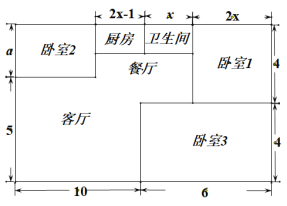
(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含![]() 的代数式表示)?
的代数式表示)?
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有![]() 两种活动方案,如表:
两种活动方案,如表:
活动方案 | 木地板价格 | 地砖价格 | 总安装费 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?