题目内容
【题目】如图,在平面直角坐标系xOy中,点C的坐标为(4,0),一次函数 ![]() 的图像分别交x轴、y轴于点A、点B.
的图像分别交x轴、y轴于点A、点B.
(1)若点D是直线AB在第一象限内的点,且BD=BC,试求出点D的坐标.
(2)在⑴的条件下,若点Q是坐标轴上的一个动点,试探索在第一象限是否存在另一个点P,使得以B、D、P、Q为顶点的四边形是菱形(BD为菱形的一边)?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】
(1)解:如图1,设点D(3a,4a+3),
过点D作DE⊥y轴于E,把x=0代入y= ![]() x+3中,得,y=3,
x+3中,得,y=3,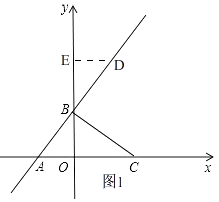
∴OB=3,
∴BE=OE-OB=4a+3-3=4a,BC= ![]() =5,
=5,
在Rt△BED中,根据勾股定理得,(3a)2+(4a)2=52 ,
∴a=±1,
∵点D在第一象限,
∴a=1,
∴D(3,7)
(2)解:由(1)知,BD=BC=5,
①当点Q在y轴上时,
设Q(0,q),
∵使得以B,D,P,Q为顶点的四边形是菱形(BD为菱形的一边),且点P在第一象限内,
即:四边形BDPQ是菱形,
∴PQ∥BD,DP∥BQ,
∴点P的横坐标为3,
∵四边形BDPQ是菱形,
∴BQ=BD=5,
∵B(0,3),
∴Q(0,8)或(0,-2),
Ⅰ、当点Q(0,8)时,
∵直线BD的解析式为y= ![]() x+3,
x+3,
∴直线PQ的解析式为y= ![]() x+8,
x+8,
当x=3时,y=12,
∴P(3,12),
Ⅱ、点Q(0,-2)时,
∵直线BD的解析式为y= ![]() x+3,
x+3,
∴直线PQ的解析式为y= ![]() x-2,
x-2,
当x=3时,y=2,
∴P(3,2),
②当点Q在x轴上时,
设Q(m,0),),
∵使得以B,D,P,Q为顶点的四边形是菱形(BD为菱形的一边),且点P在第一象限内,
即:四边形BDPQ是菱形,
∴BQ=BD=5,
∵OB=3,
∴OQ=4,
∴Q(-4,0)或(4,0)
Ⅰ、当Q(-4,0)时,∵一次函数y= ![]() x+3的图象交x轴于点A,
x+3的图象交x轴于点A,
∴A(- ![]() ,0),
,0),
∴点Q在点A的左侧,
∴点P在第二象限内,不符合题意,舍去,
Ⅱ、当点Q(4,0)时,∵四边形BDPQ是菱形,
∴BQ∥DP,PQ∥BD,
∵直线BD的解析式为y= ![]() x+3,
x+3,
∴设直线PQ的解析式为y= ![]() x+b,
x+b,
∴ ![]() ×4+b=0,
×4+b=0,
∴b=- ![]() ,
,
∴直线PQ的解析式为y= ![]() x-
x- ![]() ①,
①,
∵B(0,3),Q(4,0),
∴直线BQ的解析式为y=- ![]() x+3,
x+3,
∵D(3,7),
∴直线DP的解析式为y=- ![]() x+
x+ ![]() ②,
②,
联立①②解得,x=7,y=4,
∴P(7,4),
即:满足条件的点P的坐标为(3,12)、(3,2)、(7,4).
【解析】(1)过点D作DE⊥y轴于E,先求出直线AB与y轴的交点坐标,再根据勾股定理求出BC的长,然后在Rt△BED中用勾股定理建立方程求出a的值,就可求得点D的坐标。
(2)分两种情况讨论:①当点Q在y轴上时,利用菱形的性质求出BQ=5,再求出点Q的坐标为(0,8)或(0,-2),然后利用菱形的性质求出当点Q为(0,8)和(0,-2)时的点P的坐标;②当点Q在x轴上时,先求出点Q的坐标为(-4,0)或(4,0),然后利用菱形的性质分别求出点Q的坐标为(-4,0)和(4,0)时的点P的坐标。

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】下表是一组二次函数y=x2+3x﹣5的自变量x与函数值y的对应值:
x | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
y | ﹣1 | ﹣0.49 | 0.04 | 0.59 | 1.16 |
那么方程x2+3x﹣5=0的一个近似根是( )
A.1
B.1.1
C.1.2
D.1.3
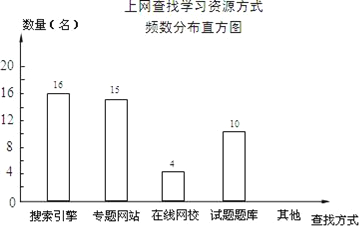
【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
上网查找学习资源方式频数分布表
查找方式 | 频数 | 频率 |
搜索引擎 | 16 | 32% |
专题网站 | 15 | a |
在线网校 | 4 | 8% |
试题题库 | 10 | 20% |
其他 | b | 10% |
(1)频数分布表中a,b的值:a= ;b= ;
(2)补全频数分布直方图;
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?