题目内容
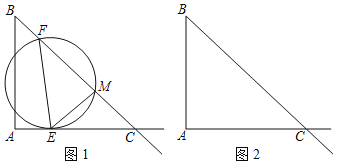
【题目】在正方形ABCD中,点E是BC边上一点,连接AE.
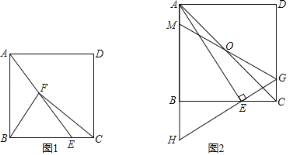
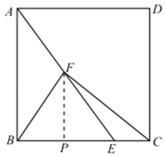
(1)如图1,点F为AE的中点,连接CF.已知tan∠FBE=![]() ,BF=5,求CF的长;
,BF=5,求CF的长;
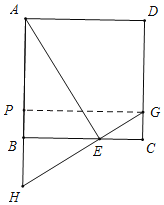
(2)如图2,过点E作AE的垂线交CD于点G,交AB的延长线于点H,点O为对角线AC的中点,连接GO并延长交AB于点M,求证:AM+BH=BE.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)根据直角三角形的性质得到BF,作FP⊥BC于点P,利用tan∠FBE=![]() 求出PF,再利用勾股定理求出CF;
求出PF,再利用勾股定理求出CF;
(2)先证明△AMO≌△CGO得到AM=GC,过G作GP垂直AB于点P,根据矩形的性质得到AB=PG,再证明△ABE≌△GPH即可得到结论.
解:(1)Rt△ABE中,BF为中线,BF=5,
∴AE=10,FE=5,
作FP⊥BC于点P,
Rt△BFP中,BF=5, ![]() ,
,
∴BP=3,FP=4,
在等腰三角形△BFE中,BE=2BP=6,
由勾股定理求得![]() ,
,
∴CP=8﹣3=5,
∴![]() ;
;
(2)∵∠ACD=∠BAC=45°,AO=CO,∠AOM=∠COG,
∴△AMO≌△CGO(ASA),
∴AM=GC,
过G作GP垂直AB于点P,得矩形BCGP,
∴CG=PB,
∵AB=PG,∠AEB=∠H,∠ABE=∠GPH,
∴△ABE≌△GPH(ASA),
∴BE=PH=PB+BH=CG+BH=AM+BH.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目