题目内容
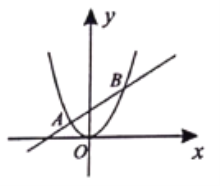
【题目】如图所示,抛物线![]() 与直线
与直线![]() 交于两点
交于两点![]() .已知点
.已知点![]() 坐标为
坐标为![]()
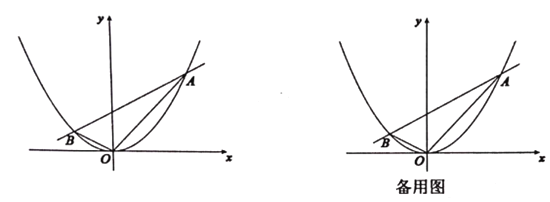
(1)求![]() 点坐标;
点坐标;
(2)求![]() 的面积;
的面积;
(3)将直线![]() 从原点出发向上平移
从原点出发向上平移![]() 个单位,设
个单位,设![]() 为直线平移后其上一点,且满足
为直线平移后其上一点,且满足![]() ,试求
,试求![]() 的值.
的值.
【答案】(1)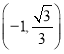 ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)将点A分别代入抛物线表达式和直线表达式,求出a和b,从而联立方程组求出点B坐标;
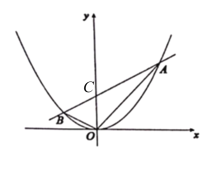
(2)设直线与y轴交于点C,求出直线与y轴交点坐标得出△BOC和△AOC的公共底,再利用面积公式求出△AOB的面积;
(3)列出平移后的表达式,得到点C坐标,过点A,B分别作![]() 轴的平行线,交x轴于G,F点,交过C点与x轴平行的直线于E,D两点,证明
轴的平行线,交x轴于G,F点,交过C点与x轴平行的直线于E,D两点,证明![]() ,得出
,得出![]() ,
,![]() ,由
,由![]() ,
,![]() 得出方程组,解之即可.
得出方程组,解之即可.
解:(1)∵抛物线![]() 与直线
与直线![]() 交于两点A、B,
交于两点A、B,
且![]() 点坐标为
点坐标为![]() ,将点A代入
,将点A代入![]() ,
,
可得![]() ,
,
解得![]() ,
,
![]() 抛物线为
抛物线为![]() ,
,
将点A代入![]() ,
,
解得![]() ,
,
![]() 直线为
直线为![]() ,
,
联立方程组,
解得![]()
![]() 或
或![]() ,
,![]() ,
,
![]() 点坐标为
点坐标为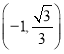 ;
;
(2)设直线与y轴交于点C,
设![]() ,代入
,代入![]() ,
,
得![]() ,
,
则![]() ;
;
(3)∵将直线![]() 从原点出发向上平移
从原点出发向上平移![]() 个单位,
个单位,
![]() 平移后的直线的解析式为
平移后的直线的解析式为![]()
设![]() 点坐标为
点坐标为![]() ,
,
过点![]() 分别作
分别作![]() 轴的平行线,交
轴的平行线,交![]() 轴于
轴于![]() 点,交过
点,交过![]() 点与
点与![]() 轴平行的直线于
轴平行的直线于![]() 两点,
两点,
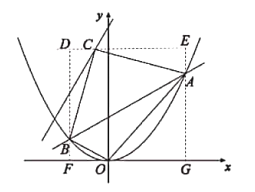
∵∠ACB=90°,∠D=90°,
∴∠DCB+∠ACE=90°,∠ACE+∠EAC=90°,
∴∠DCB=∠EAC,
又![]() ,
,
在△ACE和△CBD中,
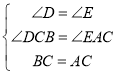 ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() 由
由![]()
得![]() ,
,
由![]() ,
,
得![]() ,
,
解得![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目