Question

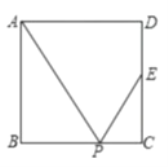
【题目】如图，Rt△ABC中，AB＝6，AC＝8．动点E，F同时分别从点A，B出发，分别沿着射线AC和射线BC的方向均以每秒1个单位的速度运动，连接EF，以EF为直径作⊙O交射线BC于点M，连接EM，设运动的时间为t（t＞0）．

（1）当点E在线段AC上时，用关于t的代数式表示CE＝　 　，CM＝　 　．（直接写出结果）

（2）在整个运动过程中，当t为何值时，以点E、F、M为顶点的三角形与以点A、B、C为顶点的三角形相似？

Answer 1

【答案】(1)8-t, ;(2) t的值为s或s．

【解析】

（1）当点E在线段AC上时，0＜t≤8．根据题意，可知AE=t，则CE=AC-AE=8-t，利用圆周角定理得∠EMF=90°．则可证得△CEM∽△CBA，利用相似比可表示出CM；
（2）讨论：当E点在线段AC上，（0＜t≤8），先由△CEM∽△CBA，利用相似比可表示出，则FM=，①若∠EFM=∠B时，△MFE∽△ABC，利用相似比可求出t=0（舍去）；②若∠EFM=∠ACB时，△MEF∽△ABC，利用相似比可求得t=（s）；分情况进行讨论即可；

解：（1）如图1中，当点 E 在线段 AC 上时，0＜t≤8．根据题意，可知 AE＝t，则 CE＝AC﹣AE＝8﹣t．

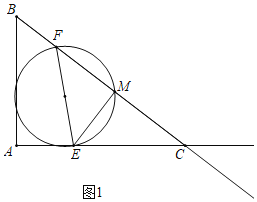
∵EF 为直径，

∴∠EMF＝90°．

∵∠ECM＝∠BCA，

∴△CEM∽△CBA，

∴，即，

∴，

故答案为：8﹣t，．

（2）∵△CEM∽△CBA，

∴，

即，

解得，

∴FM＝BC﹣BF﹣CM＝10﹣t﹣＝，

当E点在线段 AC 上，（0＜t≤8），

①如图1中，若∠EFM＝∠B时，△MFE∽△ABC，

∴，

即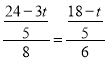，解得t＝0（舍去）．

②若∠EFM＝∠ACB时，△MEF∽△ABC，

∴

即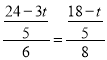，解得t＝（成立）．

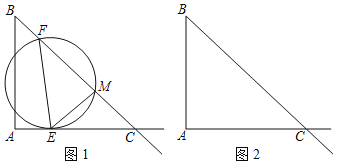
当E点在线段AC的延长线上，8＜t≤10，如图2中，

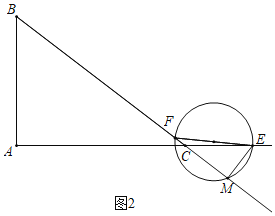
显然EM＜CM≤FM，∴△MFE∽△ABC不成立，

只有△MFE∽△ACB，当点F运动到C点时，

∵∠EFM＝∠ACB，∠CME＝∠A，

∴△MEF∽△ABC，此时t＝10（成立）；

当t＞10时，由题意ME＝（t﹣8），FM＝BC+CM﹣BF＝10+（8﹣t）﹣t＝，

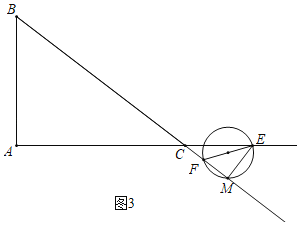
若△MFE∽△ABC，此时∠EFM＝∠B，则＝，即（8﹣t）：＝3：4，

解得t＝（成立），

若△MEF∽△ABC，此时∠EFM＝∠ACB，则＝，即（t﹣8）：＝3：4，

解得t＝10（舍弃），

综上所述，满足条件的t的值为s或s．