题目内容
【题目】已知:抛物线![]()
![]() 的顶点为A,与x轴的交点为B,C(点B在点C的左侧).
的顶点为A,与x轴的交点为B,C(点B在点C的左侧).
(1)直接写出抛物线对称轴方程;
(2)若抛物线经过原点,且△ABC为直角三角形,求a,b的值;
(3)若D为抛物线对称轴上一点,则以A,B,C,D为顶点的四边形能否为正方形?若能,请写出a,b满足的关系式;若不能,说明理由.
【答案】(1)抛物线对称轴方程:![]() .(2)
.(2)![]() ,
,![]() 或
或![]() ,
,![]() .(3)
.(3)![]() .
.
【解析】
(1)根据y=a(x-2)2+b直接得出答案;
(2)根据直线x=2与x轴交于点E,则E(2,0),以及抛物线经过原点,得出B(0,0),C(4,0),进而求出AE=BE=EC,当抛物线的顶点为A(2,-2)时,以及当抛物线的顶点为A′(2,2)时求出即可;
(3)根据B、C关于点E中心对称,当A,D也关于点E对称,且BE=AE时,四边形ABDC是正方形,即可求出.
(1)抛物线对称轴方程:直线x=2.
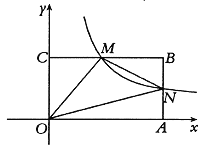
(2)如图,
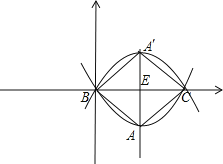
设直线x=2与x轴交于点E,则E(2,0).
∵抛物线经过原点,
∴B(0,0),C(4,0).(3分)
∵△ABC为直角三角形,根据抛物线的对称性可知AB=AC,
∴AE=BE=EC,
∴A(2,-2)或(2,2).
当抛物线的顶点为A(2,-2)时,y=a(x-2)2-2,
把(0,0)代入,得:a=![]() ,
,
此时,b=-2.
当抛物线的顶点为A′(2,2)时,y=a(x-2)2+2,
把(0,0)代入,得:a=![]() ,此时,b=2.
,此时,b=2.
∴a=![]() ,b=-2或a=
,b=-2或a=![]() ,b=2.
,b=2.
(3)依题意,B、C关于点E中心对称,当A,D也关于点E对称,且BE=AE时,四边形ABDC是正方形.
∵A(2,b),
∴AE=|b|,
∴B(2-|b|,0),
把B(2-|b|,0)代入y=a(x-2)2+b,得ab2+b=0,
∵b≠0,
∴abb+b=0,
∴b=-ab2,即![]() =-1,-ab=1,
=-1,-ab=1,
∴ab=-1.

 阅读快车系列答案
阅读快车系列答案【题目】当行驶中的汽车撞到物体时,汽车的损坏程度通常用“撞击影响”来衡量.汽车的撞击影响I可以用汽车行驶速度v(km/min)来表示,下表是某种型号汽车的行驶速度与撞击影响的试验数据:
v(km/min) | 0 | 1 | 2 | 3 | 4 |
I | 0 | 2 | 8 | 18 | 32 |
(1)请根据上表中的数据,在直角坐标系中描出坐标(v,I)所对应的点,并用光滑曲线将各点连接起来;

(2)填写下表,并根据表中数据的呈现规律,猜想用v表示I的二次函数表达式;
v(km/min) | 1 | 2 | 3 | 4 |
|
|
|
|
|
(3)当汽车的速度分别是1.5 km/min,2.5 km/min,4.5 km/min时,利用你得到的撞击影响公式,计算撞击影响分别是多少?