题目内容
如图,已知抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,3).
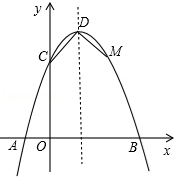
(1)求抛物线的解析式;
(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点M是抛物线上一点,以B,C,D,M为顶点的四边形是直角梯形,试求出点M的坐标.

(1)求抛物线的解析式;
(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)点M是抛物线上一点,以B,C,D,M为顶点的四边形是直角梯形,试求出点M的坐标.
解:(1)∵抛物线与y轴交于点C(0,3),
∴设抛物线解析式为y=ax2+bx+3(a≠0),
根据题意,得 ,解得
,解得 。
。
∴抛物线的解析式为y=﹣x2+2x+3。
(2)存在。
由y=﹣x2+2x+3得,D点坐标为(1,4),对称轴为x=1。
①若以CD为底边,则PD=PC,
设P点坐标为(x,y),根据勾股定理,得 ,即y=4﹣x。
,即y=4﹣x。
又P点(x,y)在抛物线上,∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0。
解得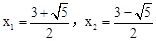 <1,舍去。
<1,舍去。
∴ ,∴
,∴ 。
。
∴点P坐标为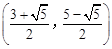 。
。
②若以CD为一腰,
∵点P在对称轴右侧的抛物线上,由抛物线对称性知,点P与点C关于直线x=1对称,
∴点P坐标为(2,3)。
综上所述,符合条件的点P坐标为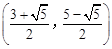 或(2,3)。
或(2,3)。
(3)由B(3,0),C(0,3),D(1,4),根据勾股定理,得CB= ,CD=
,CD= ,BD=
,BD= ,
,
∴CB2+CD2=BD2=20。∴∠BCD=90°。
设对称轴交x轴于点E,过C作CM⊥DE,交抛物线于点M,垂足为F,

在Rt△DCF中,∵CF=DF=1,∴∠CDF=45°。,
由抛物线对称性可知,∠CDM=2×45°=90°,点坐标M为(2,3)。
∴DM∥BC。∴四边形BCDM为直角梯形。
由∠BCD=90°及题意可知,
以BC为一底时,顶点M在抛物线上的直角梯形只有上述一种情况;
以CD为一底或以BD为一底,且顶点M在抛物线上的直角梯形均不存在。
综上所述,符合条件的点M的坐标为(2,3)。
∴设抛物线解析式为y=ax2+bx+3(a≠0),
根据题意,得
 ,解得
,解得 。
。∴抛物线的解析式为y=﹣x2+2x+3。
(2)存在。
由y=﹣x2+2x+3得,D点坐标为(1,4),对称轴为x=1。
①若以CD为底边,则PD=PC,
设P点坐标为(x,y),根据勾股定理,得
 ,即y=4﹣x。
,即y=4﹣x。又P点(x,y)在抛物线上,∴4﹣x=﹣x2+2x+3,即x2﹣3x+1=0。
解得
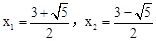 <1,舍去。
<1,舍去。∴
 ,∴
,∴ 。
。∴点P坐标为
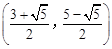 。
。②若以CD为一腰,
∵点P在对称轴右侧的抛物线上,由抛物线对称性知,点P与点C关于直线x=1对称,
∴点P坐标为(2,3)。
综上所述,符合条件的点P坐标为
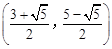 或(2,3)。
或(2,3)。(3)由B(3,0),C(0,3),D(1,4),根据勾股定理,得CB=
 ,CD=
,CD= ,BD=
,BD= ,
,∴CB2+CD2=BD2=20。∴∠BCD=90°。
设对称轴交x轴于点E,过C作CM⊥DE,交抛物线于点M,垂足为F,

在Rt△DCF中,∵CF=DF=1,∴∠CDF=45°。,
由抛物线对称性可知,∠CDM=2×45°=90°,点坐标M为(2,3)。
∴DM∥BC。∴四边形BCDM为直角梯形。
由∠BCD=90°及题意可知,
以BC为一底时,顶点M在抛物线上的直角梯形只有上述一种情况;
以CD为一底或以BD为一底,且顶点M在抛物线上的直角梯形均不存在。
综上所述,符合条件的点M的坐标为(2,3)。
试题分析:(1)由于A(﹣1,0)、B(3,0)、C(0,3)三点均在坐标轴上,故用待定系数法求解即可。
(2)分以CD为底和以CD为腰两种情况讨论.运用两点间距离公式建立起P点横坐标和纵坐标之间的关系,再结合抛物线解析式即可求解。
(3)根据抛物线上点的坐标特点,利用勾股定理求出相关边长,再利用勾股定理的逆定理判断出直角梯形中的直角。

练习册系列答案
相关题目

 ),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).

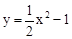 先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为
先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为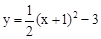
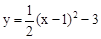
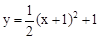

 与二次函数
与二次函数 的图象可能是
的图象可能是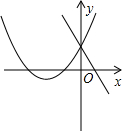
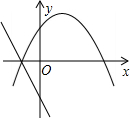
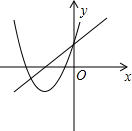

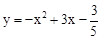 ,当自变量x取m对应的函数值大于0,设自变量分别取m-3,m+3 时对应的函数值为y1,y2,则
,当自变量x取m对应的函数值大于0,设自变量分别取m-3,m+3 时对应的函数值为y1,y2,则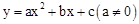 的图象如图所示,有下列5个结论:
的图象如图所示,有下列5个结论:
