题目内容
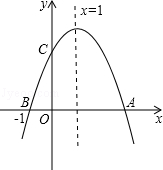
如图,抛物线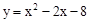 交y轴于点A,交x轴正半轴于点B.
交y轴于点A,交x轴正半轴于点B.

(1)求直线AB对应的函数关系式;
(2)有一宽度为1的直尺平行于x轴,在点A、B之间平行移动,直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ,设M点的横坐标为m,且0<m<3.试比较线段MN与PQ的大小.
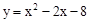 交y轴于点A,交x轴正半轴于点B.
交y轴于点A,交x轴正半轴于点B.
(1)求直线AB对应的函数关系式;
(2)有一宽度为1的直尺平行于x轴,在点A、B之间平行移动,直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ,设M点的横坐标为m,且0<m<3.试比较线段MN与PQ的大小.
(1)y=2x﹣8
(2)①当2m﹣3<0,即0<m<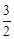 时, 则MN﹣PQ<0,即MN<PQ;
时, 则MN﹣PQ<0,即MN<PQ;
②当2m﹣3=0,即m=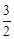 时, 则MN﹣PQ=0,即MN=PQ;
时, 则MN﹣PQ=0,即MN=PQ;
③当2m﹣3>0即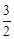 <m<3时,则MN﹣PQ>0,即MN>PQ。
<m<3时,则MN﹣PQ>0,即MN>PQ。
(2)①当2m﹣3<0,即0<m<
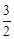 时, 则MN﹣PQ<0,即MN<PQ;
时, 则MN﹣PQ<0,即MN<PQ;②当2m﹣3=0,即m=
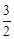 时, 则MN﹣PQ=0,即MN=PQ;
时, 则MN﹣PQ=0,即MN=PQ;③当2m﹣3>0即
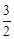 <m<3时,则MN﹣PQ>0,即MN>PQ。
<m<3时,则MN﹣PQ>0,即MN>PQ。分析:(1)利用二次函数解析式,求出A、B两点的坐标,再利用待定系数法求出一次函数解析式;
(2)根据M的横坐标和直尺的宽度,求出P的横坐标,再代入直线和抛物线解析式,求出MN、PQ的长度表达式,再比较即可。
解:(1)当x=0时,y=﹣8;
当y=0时,x2﹣2x﹣8=0,解得,x1=4,x2=﹣8。
∴A(0,﹣8),B(4,0)。
设一次函数解析式为y=kx+b,
将A(0,﹣8),B(4,0)分别代入解析式得
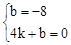 ,解得,
,解得, 。
。∴一次函数解析式为y=2x﹣8。
(2)∵M点横坐标为m,则P点横坐标为(m+1)。
∴
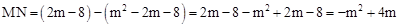 ;
;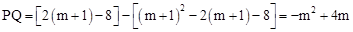 。
。∴
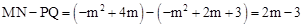 。
。∵0<m<3,
∴①当2m﹣3<0,即0<m<
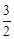 时, 则MN﹣PQ<0,即MN<PQ;
时, 则MN﹣PQ<0,即MN<PQ;②当2m﹣3=0,即m=
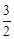 时, 则MN﹣PQ=0,即MN=PQ;
时, 则MN﹣PQ=0,即MN=PQ;③当2m﹣3>0即
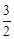 <m<3时,则MN﹣PQ>0,即MN>PQ。
<m<3时,则MN﹣PQ>0,即MN>PQ。
练习册系列答案
相关题目


 )
)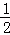 时,y的值.
时,y的值.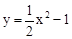 先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为
先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为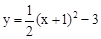
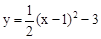
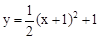

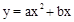 。
。 。
。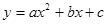 与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N。
与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N。
 ,求N点坐标;
,求N点坐标; 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与 轴交于负半轴.给出四个结论:①abc<0;②2a+
轴交于负半轴.给出四个结论:①abc<0;②2a+ >0;③a+c=1; ④a>1.其中正确结论的序号是 (将你认为正确结论的序号都填上) .
>0;③a+c=1; ④a>1.其中正确结论的序号是 (将你认为正确结论的序号都填上) .
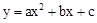 (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是