题目内容
若二次函数 (a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断正确的是
(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断正确的是
 (a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断正确的是
(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断正确的是| A.a>0 | B.b2-4ac≥0 |
| C.x1<x0<x2 | D.a(x0-x1)( x0-x2)<0 |
D
试题分析:a的符号不能确定,选项A错误。
二次函数
 (a≠0)的图象与x轴有两个交点,故b2-4ac>0。选项B错误。
(a≠0)的图象与x轴有两个交点,故b2-4ac>0。选项B错误。分a>0,a<0两种情况画出两个草图来分析(见下图):
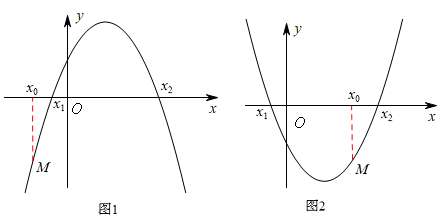
由于a的符号不能确定(可正可负,即抛物线的开口可向上,也可向下),所以x0,x1, x2的大小就无法确定。选项C错误。
在图1中,a<0且有x0<x1< x2(或x1< x2< x0),则a(x0-x1)( x0-x2)<0;在图2中a>0,且有x1< x0< x2,则a(x0-x1)( x0-x2)<0.。选项C正确。
故选D。

练习册系列答案
相关题目
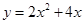 .
.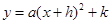 的形式(要求写出配方过程);
的形式(要求写出配方过程); .
.

 的对称轴是直线x=
的对称轴是直线x= ,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).
,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).
 的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
 与二次函数
与二次函数 的图象可能是
的图象可能是



 的最小值是 .
的最小值是 .