题目内容
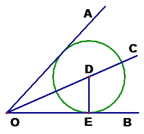
【题目】如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为【 】

A.![]() B.1 C.
B.1 C.![]() 或1 D.
或1 D.![]() 或1或
或1或![]()
【答案】D。
【解析】若△BEF是直角三角形,则有两种情况:①∠BFE=90°,②∠BEF=90°,分别讨论如下:
∵AB是⊙O的直径,∴∠ACB=90°。
Rt△ABC中,BC=2,∠ABC=60°,∴AB=2BC=4cm。
①当∠BFE=90°时;
Rt△BEF中,∠ABC=60°,则BE=2BF=2cm。
∴此时AE=AB-BE=2cm。
∵E点沿着A→B→A方向运动,∴E点运动的距离为:2cm或6cm。
∵点E以2cm/s的速度运动,∴t=1s或3s。
∵0≤t<3,∴t=3s不合题意,舍去。
∴当∠BFE=90°时,t=1s。
②当∠BEF=90°时,
同①可求得BE=![]() cm,此时AE=AB-BE=
cm,此时AE=AB-BE=![]() cm。
cm。
∵E点沿着A→B→A方向运动,∴E点运动的距离为:3.5cm或4.5cm。
∵点E以2cm/s的速度运动,∴t=![]() s或
s或![]() s(二者均在0≤t<3内)。
s(二者均在0≤t<3内)。
综上所述,当t的值为1、![]() 或
或![]() s时,△BEF是直角三角形。故选D。
s时,△BEF是直角三角形。故选D。

练习册系列答案
相关题目