题目内容
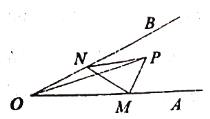
【题目】如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,
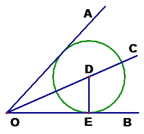
①判断⊙D与OA的位置关系, 并证明你的结论。
②通过上述证明,你还能得出哪些等量关系?
【答案】(1)⊙D与OA的位置关系是相切 ,证明详见解析;(2)∠DOA=∠DOE, OE=OF.
【解析】试题分析:(1)首先过点D作DF⊥OA于F,由点D是∠AOB的平分线OC上任意一点,DE⊥OB,根据角平分线的性质,即可得DF=DE,则可得D到直线OA的距离等于⊙D的半径DE,则可证得⊙D与OA相切.
(2)根据(1)可得:∠DOA=∠DOE, OE=OF
试题解析:(1)⊙D与OA的位置关系是相切
证明:过D作DF⊥OA于F
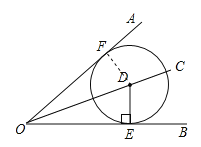
又点D是∠AOB的平分线OC上任意一点,DE⊥OB,所以DE=DF
直线OA过半径外端,又与半径垂直,所以OA是⊙D的切线.
(2)∠DOA=∠DOE, OE=OF

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目