ЬтФПФкШн
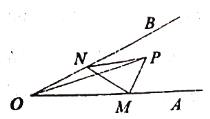
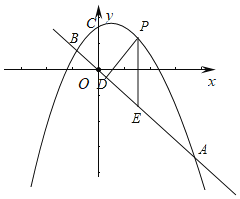
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=-x2+bx+cгыжБЯпy=-xЕФНЛЕуAЁЂBЕФКсзјБъЗжБ№ЮЊ2КЭ![]() ЃЎЕуPЪЧжБЯпЩЯЗНХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЙ§ЕуPзїPDЁЭABгкЕуDЃЌзїPEЁЭxжсНЛABгкЕуEЃЎ
ЃЎЕуPЪЧжБЯпЩЯЗНХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЙ§ЕуPзїPDЁЭABгкЕуDЃЌзїPEЁЭxжсНЛABгкЕуEЃЎ
ЃЈ1ЃЉжБНгаДГіЕуAЁЂBЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉХаЖЯЁїOBCаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ4ЃЉЩшЕуPЕФКсзјБъЮЊnЃЌЯпЖЮPDЕФГЄЮЊyЃЌЧѓyЙигкnЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ5ЃЉЖЈвхЗћКХmin{aЃЌbЃЉ}ЕФКЌвхЮЊЃКЕБaЁнbЪБЃЌmin{aЃЌb}=bЃЛЕБaЃМbЪБЃЌmin{aЃЌb}=aЃЎШчmin{2ЃЌ0}=0ЃЌmin{-3ЃЌ4}=-3ЃЎжБНгаДГіmin{-x2+bx+cЃЌ-x}ЕФзюДѓжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЃЈ2-2ЃЉЃЌЕуBЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ2ЃЉy=-x2+
ЃЉЃЛЃЈ2ЃЉy=-x2+![]() x+1ЃЛЃЈ3ЃЉЁїOBCЪЧЕШбќжБНЧШ§НЧаЮЃЎРэгЩМћНтЮіЃЛЃЈ4ЃЉy=-
x+1ЃЛЃЈ3ЃЉЁїOBCЪЧЕШбќжБНЧШ§НЧаЮЃЎРэгЩМћНтЮіЃЛЃЈ4ЃЉy=-![]() n2+
n2+![]() n+
n+![]() ЃЛЃЈ5ЃЉmin{-x2+
ЃЛЃЈ5ЃЉmin{-x2+![]() x+1ЃЌ-x}зюДѓжЕЮЊ
x+1ЃЌ-x}зюДѓжЕЮЊ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉAЁЂBЕФКсзјБъЗжБ№ЮЊ2КЭ-![]() ЃЌДњШыНтЮіЪНy=-xПЩЕУЕуAЃЌЕуBЕФзјБъЃЛ
ЃЌДњШыНтЮіЪНy=-xПЩЕУЕуAЃЌЕуBЕФзјБъЃЛ
ЃЈ2ЃЉгУД§ЖЈЯЕЪ§ЗЈПЩЧѓНтЮіЪНЃЛ
ЃЈ3ЃЉгЩИљОнСНЕуОрРыЙЋЪНПЩЧѓOBЃЌOCЃЌBCЕФГЄЖШЃЌПЩЕУBC=OBЃЌИљОнЙДЙЩЖЈРэФцЖЈРэПЩХаЖЯЁЯOBC=90ЁуЃЌМДПЩЧѓЁїOBCаЮзДЃЛ
ЃЈ4ЃЉгЩЕуPЕФКсзјБъЮЊnЃЌПЩЧѓPE=-n2+![]() n+1ЃЌИљОнЬтвтПЩЧѓЁЯBOC=45Ёу=ЁЯPEDЃЌИљОнЙДЙЩЖЈРэПЩЧѓPD=y=
n+1ЃЌИљОнЬтвтПЩЧѓЁЯBOC=45Ёу=ЁЯPEDЃЌИљОнЙДЙЩЖЈРэПЩЧѓPD=y=![]() PEЃЌМДПЩЧѓyЙигкnЕФКЏЪ§ЙиЯЕЪНЃЛ
PEЃЌМДПЩЧѓyЙигкnЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ5ЃЉЗжЂй-x2+![]() x+1Ён-xЪБЃЌЂк-x2+
x+1Ён-xЪБЃЌЂк-x2+![]() x+1ЃМ-xЪБЃЌСНжжЧщПіЬжТлЃЌПЩЧѓmin{-x2+
x+1ЃМ-xЪБЃЌСНжжЧщПіЬжТлЃЌПЩЧѓmin{-x2+![]() x+1ЃЌ-x}зюДѓжЕЃЎ
x+1ЃЌ-x}зюДѓжЕЃЎ
ЃЈ1ЃЉЁпAЁЂBЕФКсзјБъЗжБ№ЮЊ2КЭ![]() ЃЌЧвЕуAЃЌЕуBдкжБЯпy=-xЩЯЃЌ
ЃЌЧвЕуAЃЌЕуBдкжБЯпy=-xЩЯЃЌ
ЁрAЃЈ2-2ЃЉЃЌЕуBЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЃЈ2ЃЉЁпХзЮяЯпy=-x2+bx+cОЙ§ЕуAЃЌЕуBЃЌ
Ёр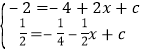 ЃЌ
ЃЌ
НтЕУЃКb=![]() ЃЌc=1ЃЌ
ЃЌc=1ЃЌ
ЁрХзЮяЯпНтЮіЪНy=-x2+![]() x+1ЃЌ
x+1ЃЌ
ЃЈ3ЃЉЁїOBCЪЧЕШбќжБНЧШ§НЧаЮЃЎ
РэгЩШчЯТЃКЁпХзЮяЯпy=-x2+![]() x+1гыyжсНЛгкЕуCЃЌ
x+1гыyжсНЛгкЕуCЃЌ
ЁрЕБx=0ЪБЃЌдђy=1ЃЌ
МДЕуCзјБъЃЈ0ЃЌ1ЃЉЃЌ
гжЁпЕуOЃЈ0ЃЌ0ЃЉЃЌЕуBЃЈ-![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрOC=1ЃЌ
OB=![]() =
=![]() ЃЌ
ЃЌ
BC=![]() =
=![]() ЃЌ
ЃЌ
ЁрOB=BCЃЌ
ЁпOB2+BC2=1ЃЌOC2=1ЃЌ
ЁрOB2+BC2=OC2ЃЎ
ЁрЁЯCBO=90Ёу.
ЁрЁїOBCЪЧЕШбќжБНЧШ§НЧаЮЃЎ
ЃЈ4ЃЉЁпЕуPЕФКсзјБъЮЊnЃЌ
ЁрЕуPЃЈnЃЌ-n2+![]() n+1ЃЉЃЌЕуEЕФзјБъЃЈnЃЌ-nЃЉЃЌ
n+1ЃЉЃЌЕуEЕФзјБъЃЈnЃЌ-nЃЉЃЌ
ЁрPE=-n2+![]() n+1-ЃЈ-nЃЉ=-n2+
n+1-ЃЈ-nЃЉ=-n2+![]() n+1ЃЌ
n+1ЃЌ
ЁпжБЯпy=-xгыxжсЫљГЩШёНЧЮЊ45ЁуЃЌ
ЁрЁЯBOC=45ЁуЃЌ
ЁпPEЁЮyжсЃЌ
ЁрЁЯPED=ЁЯBOC=45ЁуЃЌЧвPDЁЭABЃЌ
ЁрPE=![]() PDЃЌ
PDЃЌ
Ёрy=![]() PE=
PE=![]() ЃЈ-n2+
ЃЈ-n2+![]() n+1ЃЉ=-
n+1ЃЉ=-![]() n2+
n2+![]() n+
n+![]() ЃЌ
ЃЌ
ЃЈ5ЃЉ![]() ЃЌ
ЃЌ
Ђй-x2+![]() x+1Ён-xЪБЃЌmin{-x2+
x+1Ён-xЪБЃЌmin{-x2+![]() x+1ЃЌ-x}=-xЃЌ
x+1ЃЌ-x}=-xЃЌ
МД-x2+![]() x+1Ён-xЃЌ
x+1Ён-xЃЌ
НтЕУЃК-![]() ЁмxЁм2ЃЌ
ЁмxЁм2ЃЌ
Ёр-2Ёмmin{-x2+![]() x+1ЃЌ-x}Ём
x+1ЃЌ-x}Ём![]() ЃЌ
ЃЌ
Ђк-x2+![]() x+1ЃМ-xЪБЃЌmin{-x2+
x+1ЃМ-xЪБЃЌmin{-x2+![]() x+1ЃЌ-x}=-x2+
x+1ЃЌ-x}=-x2+![]() x+1ЃЌ
x+1ЃЌ
МД-x2+![]() x+1ЃМ-xЃЌ
x+1ЃМ-xЃЌ
НтЕУЃКxЃМ-![]() КЭxЃО2ЃЌ
КЭxЃО2ЃЌ
ЕБxЃМ-![]() ЪБЃЌmin{-x2+
ЪБЃЌmin{-x2+![]() x+1ЃЌ-x}ЃМ
x+1ЃЌ-x}ЃМ![]() ЃЌ
ЃЌ
ЕБxЃО2ЪБЃЌmin{-x2+![]() x+1ЃЌ-x}ЃМ-2ЃЌ
x+1ЃЌ-x}ЃМ-2ЃЌ
злЩЯЫљЪіЃКmin{-x2+![]() x+1ЃЌ-x}зюДѓжЕЮЊ
x+1ЃЌ-x}зюДѓжЕЮЊ![]() .
.