题目内容
(6分).已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
(1) k ≤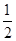 ,(2)-3
,(2)-3
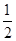 ,(2)-3
,(2)-3分析:(1)方程有两个实数根,可得△=b2-4ac≥0,代入可解出k的取值范围;
(2)结合(1)中k的取值范围,由题意可知,x1+x2=2(k-1)<0,去绝对值号结合等式关系,可得出k的值.
解答:解:(1)由方程有两个实数根,可得
△=b2-4ac=4(k-1)2-4k2=4k2-8k+4-4k2=-8k+4≥0,
解得,k≤
 ;
;(2)依据题意可得,x1+x2=2(k-1),x1?x2=k2,
由(1)可知k≤
 ,
,∴2(k-1)<0,x1+x2<0,
∴-x1-x2=-(x1+x2)=x1?x2-1,
∴-2(k-1)=k2-1,
解得k1=1(舍去),k2=-3,
∴k的值是-3.
答:(1)k的取值范围是k≤
 ;(2)k的值是-3.
;(2)k的值是-3.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
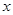 ,由题意可列方程为__________________
,由题意可列方程为__________________ ;②
;② ③
③ ;④
;④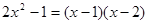 ;⑤
;⑤ ,其中一元二次方程有…………………………【 】
,其中一元二次方程有…………………………【 】 的方程
的方程 有两个不相等的实数根,则k的取值范是 .
有两个不相等的实数根,则k的取值范是 .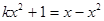 无实根,则
无实根,则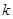 ___ ___
___ ___ (配方法); (5分)
(配方法); (5分) 