题目内容
如图，以△ABC的边BC为直径作半圆⊙O，交AB、AC分别于D、E，若直径BC=1，则sin∠ABE的值等于线段
- A.AD的长
- B.AE的长
- C.DE的长
- D.BE的长
C
分析：根据直径所对的圆周角是直角得∠BEC=∠BEA=90°；根据三角函数定义得sin∠ABE=AE：AB；根据圆内接四边形的外角等于内对角可以证明△AED∽△ABC，得对应边成比例后解答．
解答：∵BC是直径，∴∠BEC=∠BEA=90°．
∴sin∠ABE=AE：AB．
∵四边形BCED内接于圆，
∴∠ADE=∠C．
又∠A公共，
∴△AED∽△ABC．
∴AE：AB=DE：BC=DE：1=DE．
故选C．
点评：此题考查圆周角定理、三角函数定义、圆内接四边形性质、相似三角形的判定与性质等知识点，综合性较强．
分析：根据直径所对的圆周角是直角得∠BEC=∠BEA=90°；根据三角函数定义得sin∠ABE=AE：AB；根据圆内接四边形的外角等于内对角可以证明△AED∽△ABC，得对应边成比例后解答．
解答：∵BC是直径，∴∠BEC=∠BEA=90°．
∴sin∠ABE=AE：AB．
∵四边形BCED内接于圆，
∴∠ADE=∠C．
又∠A公共，
∴△AED∽△ABC．
∴AE：AB=DE：BC=DE：1=DE．
故选C．
点评：此题考查圆周角定理、三角函数定义、圆内接四边形性质、相似三角形的判定与性质等知识点，综合性较强．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
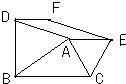26、如图，以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE，四边形ADFE是平行四边形．
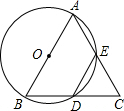如图，以△ABC的边AB为直径作⊙O，交BC于D点，交AC于E点，BD=DE
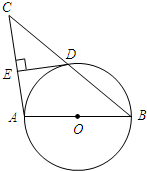（2011•峨眉山市二模）如图，以△ABC的边AB为直径作⊙O，BC与⊙O交于D，D是BC的中点，过D作DE⊥AC，交AC于点E．
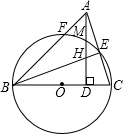（2010•黔东南州）如图，以△ABC的边BC为直径作⊙O分别交AB，AC于点F．点E，AD⊥BC于D，AD交于⊙O于M，交BE于H．
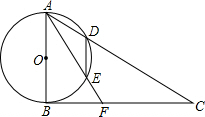如图，以△ABC的边AB为直径的⊙O交AC于点D，弦DE∥AB，∠C=∠BAF