Question

（2011•峨眉山市二模）如图，以△ABC的边AB为直径作⊙O，BC与⊙O交于D，D是BC的中点，过D作DE⊥AC，交AC于点E．
（1）求证：DE是⊙O的切线；
（2）若AB=10，BD=8，求DE的长．

Answer 1

分析：（1）要证明切线，结合DE⊥AC，只需证明OD∥AC，显然根据三角形的中位线定理即可证明；
（2）连接AD，因为AB为圆的直径，所以∠ADB=90°利用勾股定理求出AD的长，根据（1）中的平行，易证明角相等．从而发现等腰三角形ABC，然后进行计算即可．

解答：（1）证明：连接OD；
∵BD=CD，AO=B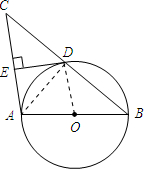O，
∴OD∥AC．
∵DE⊥AC，
∴OD⊥DE．
∴DE与⊙O相切；

（2）解：连接AD，
由（1）知，OD∥AC，
∴∠BDO=∠C．
∵OD=OB，
∴∠B=∠BDO，
∴∠B=∠C．
∴AC=AB．
∵AB=10，
∴AC=10，
∵AB为圆的直径，
∴∠ADB=90°，
∴AD=

AB 2-BD 2

=6，
∴CD=8，
∵S_△ADC=

1

2

CD×AD=

1

2

AC×DE，
∴DE=

CD•AD

AC

=

8×6

10

=4.8．

点评：本题综合性较强，考查点较多，考查了切线的判定定理和性质定理、勾股定理，以及三角形的面积公式，要细心思考认真分析，思路还是比较好找的．