题目内容
（2010•黔东南州）如图，以△ABC的边BC为直径作⊙O分别交AB，AC于点F．点E，AD⊥BC于D，AD交于⊙O于M，交BE于H．求证：DM2=DH•DA．
分析：首先利用相似三角形的判定得出△BDM∽△MDC，即可得出MD2=BD•CD，进而得出△BDH∽ADC，以及BD•CD=AD•DH，即可得出答案．
解答：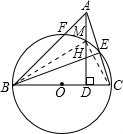
证明：连接BM，CM，
∵BC为⊙O直径，
∴∠BMC=∠BEC=90°，
∵MD⊥BC，
∴∠C+∠CMD=90°，
∵∠CMD+∠BMD=90°，
∴∠MCD=∠BMD，
∠MDC=∠MDB=90°，
∴△BDM∽△MDC，
∴
=
，
∴MD2=BD•CD，
∵∠AHE=∠BHD，∠AEH=∠HDB=90°，
∴∠DBH=∠DAC，
∠BDH=∠ADC=90°，
∴△BDH∽△ADC，
∴
=
，
∴BD•CD=AD•DH，
∴DM2=DH•DA．
证明：连接BM，CM，∵BC为⊙O直径，
∴∠BMC=∠BEC=90°，
∵MD⊥BC，
∴∠C+∠CMD=90°，
∵∠CMD+∠BMD=90°，
∴∠MCD=∠BMD，
∠MDC=∠MDB=90°，
∴△BDM∽△MDC，
∴
| BD |
| MD |
| MD |
| CD |
∴MD2=BD•CD，
∵∠AHE=∠BHD，∠AEH=∠HDB=90°，
∴∠DBH=∠DAC，
∠BDH=∠ADC=90°，
∴△BDH∽△ADC，
∴
| BD |
| AD |
| DH |
| DC |
∴BD•CD=AD•DH，
∴DM2=DH•DA．
点评：此题主要考查了相似三角形的判定与性质以及圆周角定理等知识，根据已知得出△BDM∽△MDC，△BDH∽ADC进而得出比例式是解题关键．
练习册系列答案
相关题目
（2010•黔东南州）如图，若Rt△ABC，∠C=90°，CD为斜边上的高，AC=m，AB=n，则△ACD的面积与△BCD的面积比
（2010•黔东南州）将宽为2cm的长方形折叠成如图所示的形状，那么折痕AB的长是（ ）