题目内容
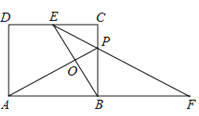
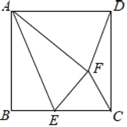
【题目】如图,正方形ABCD的边长为6,点E边BC上,连接AE,将△ABE沿着AE翻折到△AEF,连接CF、DF,若△CDF为等腰三角形,则△CDF的面积为_____.
【答案】![]() 或9.
或9.
【解析】
依据等腰三角形的定义,分三种情况:①![]() ,如图1(见解析),先根据正方形的性质、三角形全等的判定定理与性质得出
,如图1(见解析),先根据正方形的性质、三角形全等的判定定理与性质得出![]() ,从而得出
,从而得出![]() 是等边三角形,再根据等边三角形的性质求出FH、FM的长,然后根据三角形的面积公式即可得;②
是等边三角形,再根据等边三角形的性质求出FH、FM的长,然后根据三角形的面积公式即可得;②![]() ,如图2(见解析),先同理证出
,如图2(见解析),先同理证出![]() ,再根据三角形全等的性质可得
,再根据三角形全等的性质可得![]() ,然后根据三角形的面积公式即可得;③
,然后根据三角形的面积公式即可得;③![]() ,根据等腰三角形的定义、翻折的性质得出不存在这样的等腰
,根据等腰三角形的定义、翻折的性质得出不存在这样的等腰![]() 即可.
即可.
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]()
由等腰三角形的定义,分以下三种情况:
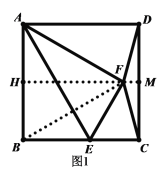
①如图1,![]() ,
,![]() 是等腰三角形,连接BF
是等腰三角形,连接BF
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
由翻折的性质得,![]()
![]() ,则
,则![]() 是等边三角形
是等边三角形
过点F作![]() ,并延长HF交CD于点M,则
,并延长HF交CD于点M,则![]()
![]() 四边形BCMH是矩形
四边形BCMH是矩形
![]()
在等边![]() 中,
中,![]()
![]()
![]()
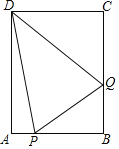
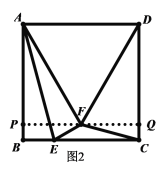
②如图2,![]() ,
,![]() 是等腰三角形
是等腰三角形
由翻折、正方形的性质得,![]()
![]()
![]() ,即
,即![]()
过点F作![]() ,并延长PF交CD于点Q,则
,并延长PF交CD于点Q,则![]()
在![]() 和
和![]() 中,
中,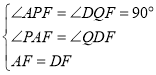
![]()
![]()
![]()
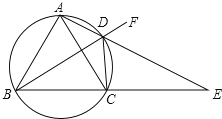
③如图3,若![]() ,
,![]() 是等腰三角形,此时点F在以点C为圆心,CD为半径的圆上;但根据翻折的性质知,
是等腰三角形,此时点F在以点C为圆心,CD为半径的圆上;但根据翻折的性质知,![]() ,即点F在以点A为圆心,AB为半径的圆上
,即点F在以点A为圆心,AB为半径的圆上
由图可知,在正方形内部,这两段圆弧没有交点,即不存在这样的点F
故不存在以CF、CD为腰的等腰![]()
综上,![]() 的面积为
的面积为![]() 或9
或9
故答案为:![]() 或9.
或9.


练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
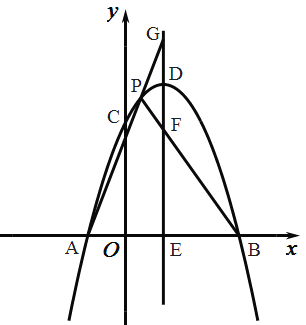
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
|
| -3 | -2 | -1 | 0 | 1 |
|
|
| 0 | 4 | 3 | 0 |
|
(1)把表格填写完整;
(2)根据上表填空:
①抛物线与![]() 轴的交点坐标是________和__________;
轴的交点坐标是________和__________;
②在对称轴右侧,![]() 随
随![]() 增大而_______________;
增大而_______________;
③当![]() 时,则
时,则![]() 的取值范围是_________________;
的取值范围是_________________;
(3)请直接写出抛物线![]() 的解析式.
的解析式.