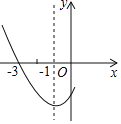Question

【题目】抛物线上部分点的横坐标，纵坐标的对应值如下表：

		-3	-2	-1	0	1
		0		4	3	0

(1)把表格填写完整；

(2)根据上表填空：

①抛物线与轴的交点坐标是________和__________；

②在对称轴右侧，随增大而_______________；

③当时，则的取值范围是_________________；

(3)请直接写出抛物线的解析式．

Answer 1

【答案】（1）3；（2）①抛物线与轴的交点坐标是和；②随增大而减小；③的取值范围是；（3）．

【解析】

（1）利用表中对应值的特征和抛物线的对称性得到抛物线的对称轴为直线x=-1，则x=0和x=-2时，y的值相等，都为3；
（2）①利用表中y=0时x的值可得到抛物线与x轴的交点坐标；
②设交点式y=a（x+3）（x-1），再把（0，3）代入求出a得到抛物线解析式为y=-x2-2x+3，则可判断抛物线的顶点坐标为（-1，4），抛物线开口向下，然后根据二次函数的性质解决问题；③由于x=-2时，y=3；当x=2时，y=-5，结合二次函数的性质可确定y的取值范围；
（3）由（2）得抛物线解析式．

解：（1）∵x=-3，y=0；x=1，y=0，
∴抛物线的对称轴为直线x=-1，
∴x=0和x=-2时，y=3；

故答案是：3；
（2）①∵x=-3，y=0；x=1，y=0，

∴抛物线与x轴的交点坐标是（-3，0）和（1，0）；

故答案是：（-3，0）和（1，0）；
②设抛物线解析式为y=a（x+3）（x-1），
把（0，3）代入得3=-3a，解得a=-1，
∴抛物线解析式为y=-（x+3）（x-1），即y=-x2-2x+3，
抛物线的顶点坐标为（-1，4），抛物线开口向下，
∴在对称轴右侧，y随x增大而减小；

故答案是：减小；
③当x=-2时，y=3；当x=2时，y=-4-4+3=-5，当x=-1，y有最大值为4，
∴当-2＜x＜2时，则y的取值范围是-5＜y≤4．

故答案是：-5＜y≤4；
（3）由（2）得抛物线解析式为y=-x2-2x+3，
故答案是：y=-x2-2x+3．