Question

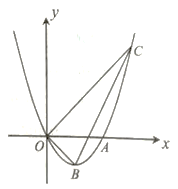
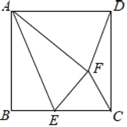
【题目】如图，四边形内接于圆，，的延长线交于点，是延长线上任意一点，．

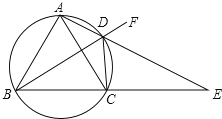
（1）求证：平分；

（2）求证：．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】

（1）根据圆内接四边形的性质得到∠CDE=∠ABC，根据圆周角定理和等腰三角形的性质证明即可；

（2）根据三角形外角的性质和图形得到∠CAE+∠E=∠ABD+∠DBC，得到∠E=∠ABD，根据圆周角定理证明即可．

（1）∵四边形ABCD内接于圆，

∴∠CDE=∠ABC．

由圆周角定理得：∠ACB=∠ADB，又∠ADB=∠FDE，

∴∠ACB=∠FDE．

∵AB=AC，

∴∠ACB=∠ABC，

∴∠FDE=∠CDE，即DE平分∠CDF；

（2）∵∠ACB=∠ABC，∠ACB=∠CAE+∠E，∠ABC=∠ABD+∠DBC，

∴∠CAE+∠E=∠ABD+∠DBC．

又∵∠CAE=∠DBC，

∴∠E=∠ABD，

∴∠ACD=∠AEB．