��Ŀ����
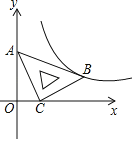
����Ŀ����ͼ������ABCD�У�AB��6cm��AD��8cm����P�ӵ�A��������ÿ��һ����λ���ٶ���A��B��C�ķ����˶���ͬʱ��Q�ӵ�B��������ÿ��2����λ���ٶ���B��C��D�ķ����˶���������һ�㵽���յ�����㶼ֹͣ�˶����������˶���ʱ��Ϊt�룮
��1����t���� ��ʱ������ֹͣ�˶���
��2������BPQ��������ΪS��ƽ����λ��
����S��t֮��ĺ�����ϵʽ��
����tΪ��ֵʱ����BPQ�������������Ƕ��٣�
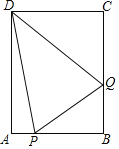
���𰸡���1��7����2���ٵ�0��t��4ʱ��S����t2+6t����4��t��6ʱ��S����4t+24����6��t��7ʱ��S��t2��10t+24����t��3ʱ����PBQ�����������ֵΪ9
��������
��1�������Q���˶�ʱ�伴���жϣ�
��2���ٵ�����ʱ��ηֱ������PBQ��������ɣ�
�����â��н��ۣ��������ʱ��ε���������ֵ�����жϣ�
�⣺��1�����ı���ABCD�Ǿ��Σ�
��AD��BC��8cm��AB��CD��6cm��
��BC+AD��14cm��
��t��14��2��7��
�ʴ�Ϊ7��
��2���ٵ�0��t��4ʱ��S��![]() ��6��t����2t����t2+6t��
��6��t����2t����t2+6t��
��4��t��6ʱ��S��![]() ��6��t����8����4t+24��
��6��t����8����4t+24��
��6��t��7ʱ��S��![]() ��t��6����2t��8����t2��10t+24��
��t��6����2t��8����t2��10t+24��
�ڵ�0��t��4ʱ��S��![]() ��6��t����2t����t2+6t������t��3��2+9��
��6��t����2t����t2+6t������t��3��2+9��
�ߩ�1��0��
��t��3ʱ����PBQ����������СֵΪ9��
��4��t��6ʱ��S��![]() ��6��t����8����4t+24��
��6��t����8����4t+24��
�ߩ�4��0��
��t��4ʱ����PBQ�����������ֵΪ8��
��6��t��7ʱ��S��![]() ��t��6����2t��8����t2��10t+24����t��5��2��1��
��t��6����2t��8����t2��10t+24����t��5��2��1��
t��7ʱ����PBQ�����������ֵΪ3��
����������t��3ʱ����PBQ�����������ֵΪ9��