题目内容
【题目】我们给出如下定义:把对角线互相垂直的四边形叫做“正交四边形”.
如图1,在四边形![]() 中,
中,![]() ,四边形
,四边形![]() 就是“正交四边形”.
就是“正交四边形”.
(1)下列四边形,一定是“正交四边形”的是______.
①平行四边形②矩形③菱形④正方形
(2)如图2,在“正交四边形”![]() 中,点
中,点![]() 分别是边
分别是边![]() 的中点,求证:四边形
的中点,求证:四边形![]() 是矩形.
是矩形.
(3)小明说:“计算‘正交四边形’的面积可以仿照菱形的方法,面积是对角线之积的一半.”小明的说法正确吗?如果正确,请给出证明;如果错误,请给出反例.
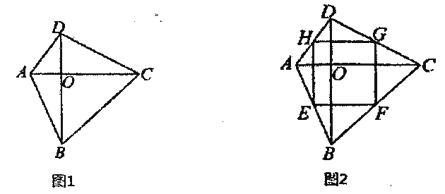
【答案】(1)③④ ;(2)详见解析;(3)小明的说法正确.
【解析】
(1)由特殊四边形的性质,可知菱形和正方形的对角线互相垂直;
(2)首先根据三角形中位线定理和平行四边形的判定定理证明四边形EFGH是平行四边形,然后再证明HG⊥HE即可;
(3)由![]() ,根据三角形的面积公式进行求解即可.
,根据三角形的面积公式进行求解即可.
答:(1)③④
(2)证明:∵![]() 分别是
分别是![]() 的中点∴
的中点∴![]() ,
,![]()
∵![]() 分别是
分别是![]() 的中点∴
的中点∴![]() ,
,![]()
∴![]() ,
,![]() .∴四边形
.∴四边形![]() 是平行四边形
是平行四边形
∵![]() 分别是
分别是![]() 的中点
的中点
∴![]()
∵四边形![]() 是“正交四边形”
是“正交四边形”
∴![]()
∴![]()
∴四边形![]() 是矩形
是矩形
(3)答:小明的说法正确.
证明:![]()
![]()

练习册系列答案
相关题目
【题目】某旅行社一则旅游消息如下:
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加一人,人均收费减少 |
(![]() )甲公司员工分两批参加该项旅游,分别支付给旅行社
)甲公司员工分两批参加该项旅游,分别支付给旅行社![]() 元和
元和![]() 元,甲公司员工有__________人.
元,甲公司员工有__________人.
(![]() )乙公司员工一起参加该项旅游,支付给旅行社
)乙公司员工一起参加该项旅游,支付给旅行社![]() 元,乙公司员工多少人?
元,乙公司员工多少人?