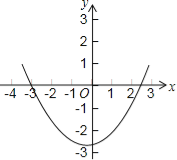题目内容
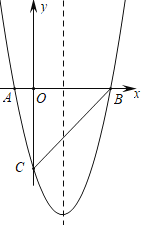
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0).B(5,0)两点,与y轴交于点C.
(1)求此物线的解析式;
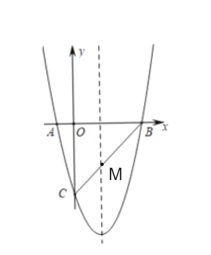
(2)在此物线的对称轴上找一点M.使得MA+MC最小,请求出点M的坐标;
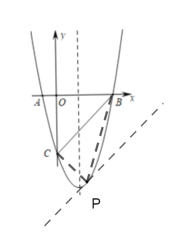
(3)在直线BC下方抛物线上是否存在点P,使得△PBC的面积最大?若存在.请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣4x﹣5;(2)M(2,﹣3);(3)存在,点P的坐标为(![]() ,
,![]() )
)
【解析】
(1)把A(﹣1,0)、B(5,0)代入抛物线y=ax2+bx﹣5求出a、b的值即可确定抛物线的关系式;
(2)由对称可得,直线BC与对称轴的交点就是所求的点M,求出直线BC的关系式和对称轴方程,求出交点坐标即可;
(3)向下平移直线BC与抛物线有唯一公共点时,这个公共点就是要求的点M,于是利用平移后的直线关系式与抛物线关系式联立,使其只有一个解时即可.
解:(1)把A(﹣1,0)、B(5,0)代入抛物线y=ax2+bx﹣5得,
![]() ,
,
解得,a=1,b=﹣4,
∴抛物线的关系式为y=x2﹣4x﹣5,
故答案为:y=x2﹣4x﹣5;
(2)当x=0时,y=﹣5,
∴点C(0,﹣5)
设直线BC的关系式为y=kx+b,
把点B、C坐标代入得,
![]() ,
,
解得,![]() ,
,
∴直线BC的关系式为y=x﹣5,
∵抛物线的关系式为y=x2﹣4x﹣5=(x﹣2)2﹣9,
∴对称轴为直线x=2,
由对称可得,直线BC与对称轴x=2交点就是所求的点M,
当x=2时,y=2﹣5=﹣3,
∴点M(2,﹣3)时,MA+MC最小,
故答案为:M(2,﹣3);
(3)向下平移直线BC,使平移后的直线与抛物线有唯一公共点P时,此时点P到BC的距离最大,因此△PBC的面积最大,
设将直线BC向下平移后的直线的关系式为y=x﹣5﹣m,
则方程x2﹣4x﹣5=x﹣5﹣m,有两个相等的实数根,
即x2﹣5x+m=0有两个相等的实数根,
∴m=![]() ,
,
当m=![]() 时,方程x2﹣5x+m=0的解为x=
时,方程x2﹣5x+m=0的解为x=![]() ,
,
把x=![]() 代入抛物线的关系式得,y=
代入抛物线的关系式得,y=![]() ﹣4×
﹣4×![]() ﹣5=﹣
﹣5=﹣![]() ,
,
∴P(![]() ,﹣
,﹣![]() )
)
答:在直线BC下方抛物线上存在点P,使得△PBC的面积最大,此时点P的坐标为(![]() ,﹣
,﹣![]() ),
),
故答案为:P(![]() ,﹣
,﹣![]() ).
).

 名校课堂系列答案
名校课堂系列答案