Question

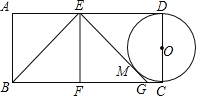
【题目】如图，在矩形ABCD中，AB＝4，AD＝8，点E、点F分别在边AD，BC上，且EF⊥AD，点B关于EF的对称点为G点，连接EG，若EG与以CD为直径的⊙O恰好相切于点M，则AE的长度为（ ）

A.3B.C.6+D.6﹣

Answer 1

【答案】D

【解析】

设AE＝x，则ED＝8﹣x，易得四边形ABFE为矩形，则BF＝x，利用对称性质得FG＝BF＝x，则CG＝8﹣2x，再根据切线长定理得到EM＝ED＝8﹣x，GM＝GC＝8﹣2x，所以EG＝16﹣3x，在Rt△EFG中利用勾股定理得到42+x2＝(16﹣3x)2，然后解方程可得到AE的长．

解：设AE＝x，则ED＝8﹣x，

∵EF⊥AD，

∴四边形ABFE为矩形，

∴BF＝x，

∵点B关于EF的对称点为G点，

∴FG＝BF＝x，

∴CG＝8﹣2x，

∵∠ADC＝∠BCD＝90°，

∴AD和BC为⊙O的切线，

∵EG与以CD为直径的⊙O恰好相切于点M，

∴EM＝ED＝8﹣x，GM＝GC＝8﹣2x，

∴EG＝8﹣x+8﹣2x＝16﹣3x，

在Rt△EFG中，42+x2＝(16﹣3x)2，

整理得x2﹣12x+30＝0，

解得x1＝6﹣，x2＝6+（舍去），

即AE的长为6﹣．

故选：D．