题目内容
【题目】甲、乙两人分别从A,B两地同时出发,匀速相向而行.甲的速度大于乙的速度,甲到达B地后,乙继续前行.设出发x h后,两人相距y km,图中折线表示从两人出发至乙到达A地的过程中y与x之间的函数关系.
根据图中信息,求:
(1)点Q的坐标,并说明它的实际意义;
(2)甲、乙两人的速度.
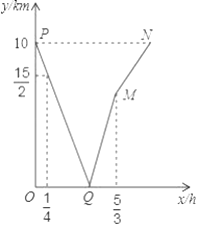
【答案】(1)点Q的坐标为(1,0),点Q的意义是:甲、乙两人分别从A,B两地同时出发后,经过1个小时两人相遇;(2)甲、乙的速度分别为6km/h、4km/h.
【解析】
(1)设PQ解析式为y=kx+b,把点P(0,10),![]() 代入所设解析式,得到
代入所设解析式,得到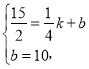 求出k、b的值,即可得出函数解析式,再根据两人相向而行,当相遇时y=0,求得x的值,即可得出点Q的坐标;
求出k、b的值,即可得出函数解析式,再根据两人相向而行,当相遇时y=0,求得x的值,即可得出点Q的坐标;
(2)分析图象,可知两人从出发到相遇用1小时,甲由相遇点到B用![]() 小时,乙走这段路程用1小时,依此可列方程组
小时,乙走这段路程用1小时,依此可列方程组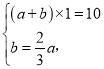 求出a、b的值,即可得出甲、乙两人的速度.
求出a、b的值,即可得出甲、乙两人的速度.
(1)设PQ解析式为y=kx+b,
把已知点P(0,10),![]() 代入得,
代入得,
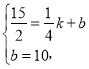
解得:![]()
∴y=-10x+10.
当y=0时,x=1,
∴点Q的坐标为(1,0),
点Q的意义是:甲、乙两人分别从A,B两地同时出发后,经过1个小时两人相遇;
(2)设甲的速度为akm/h,乙的速度为bkm/h,
由已知第![]() 小时,甲到B地,则乙走1小时路程,甲走
小时,甲到B地,则乙走1小时路程,甲走![]() 小时,
小时,
∴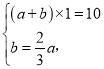
∴![]()
∴甲、乙的速度分别为6km/h、4km/h.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目