题目内容
【题目】在平面直角坐标系xOy中,反比例函数 ![]() 的图象过点A(1,6).
的图象过点A(1,6).
(1)求反比例函数的表达式;
(2)过点A的直线与反比例函数 ![]() 图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
【答案】
(1)解:∵反比例函数 ![]() 的图象过点A(1,6),
的图象过点A(1,6),
∴k=1×6=6,
∴反比例函数的表达式为:y= ![]()
(2)解:作AC⊥x轴于C,BD⊥x轴于D,
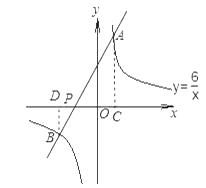
∵AC∥BD,
∴△APC∽△BPD,
∴ ![]() ,
,
∵AP=2PB,
∴AC=2BD,
∵AC=6,
∴BD=3,
∴B的纵坐标为﹣3,
代入y= ![]() 得,﹣3=
得,﹣3= ![]() ,解得x=﹣2,
,解得x=﹣2,
∴B(﹣2,﹣3),
设直线AB的解析式为y=kx+b,
∴ ![]() ,解得
,解得 ![]() ,
,
∴直线AB的解析式为y=3x+3,
令y=0,则求得x=﹣1,
∴P(﹣1,0).
【解析】将点A的坐标代入函数解析式即可求出此函数解析式。
(2)抓住关键的已知条件AP=2PB,因此作AC⊥x轴于C,BD⊥x轴于D,先证△APC∽△BPD,求出BD的长,再求出点B的坐标,然后利用待定系数法求出直线AB的函数解析式,根据y=0,求出对应的自变量的值,即可求出点P的坐标。
【考点精析】根据题目的已知条件,利用确定一次函数的表达式和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.