题目内容
如图，已知Rt△ABC中，∠ACB=90°，AC=4，BC=3，以AB边所在的直线为轴，将△ABC旋转一周，则所得几何体的表面积是（ ）A、
| ||
| B、24π | ||
C、
| ||
| D、12π |
分析：易得此几何体为两个圆锥的组合体，那么表面积为两个圆锥的侧面积，应先利用勾股定理求得AB长，进而求得圆锥的底面半径．利用圆锥的侧面积=底面周长×母线长÷2求解即可．
解答：解：AC=4，BC=3，由勾股定理得，AB=5，斜边上的高=
，
由几何体是由两个圆锥组成，∴几何体的表面积=
×2×
π×（3+4）=
π，故选C．
| 12 |
| 5 |
由几何体是由两个圆锥组成，∴几何体的表面积=
| 1 |
| 2 |
| 12 |
| 5 |
| 84 |
| 5 |
点评：本题利用了勾股定理，圆的周长公式和扇形面积公式求解．
练习册系列答案
相关题目
22、如图，已知Rt△ABC，AB=AC，∠ABC的平分线BD交AC于点D，BD的垂直平分线分别交AB，BC于点E、F，CD=CG．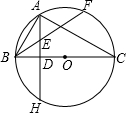
E，交⊙O于点F，且AE=BE．
5、如图，已知Rt△ABC中，∠BAC=90°，AB=AC，P是BC延长线上一点，PE⊥AB交BA延长线于E，PF⊥AC交AC延长线于F，D为BC中点，连接DE，DF．求证：DE=DF．
如图，已知Rt△ABC中，∠CAB=30°，BC=5．过点A做AE⊥AB，且AE=15，连接BE交AC于点P．
如图，已知Rt△ABC中∠A=90°，AB=3，AC=4．将其沿边AB向右平移2个单位得到△FGE，则四边形ACEG的面积为